 Bir süredir Rust tarafındaki oyun motorlarını incelemekteyim. Bu konuda sayısız youtube videosu ve öğreti buldum. Hem rust kodlama pratiklerimi geliştirmek hem de meraklı olduğum oyun programlama tekniklerini deneyimlemek için biraz zaman harcadım. Ping Pong oyunundan, uzaydaki göktaşlarını patlatan gemiye, karşısındaki farklı türden blokları onlara top fırlatarak patlatan dikdörtgenden, derin zindanlarda ortografik projeksiyon bazlı kamera kullanan sahalara neredeyse her yerde temel matematikten yararlanıldığına şahit oldum(Öğretilere ait uyguladığım pratikleri ve ortaya çıkan sonuçları game-dev-with-rust reposunda bulabilirsiniz) Bunu zaten biliyordum ama unuttuğum çekirdek matematik bilgim ile yapıldıklarını görünce aslında onlarca yıl önce öğrendiklerimin ne kadar çok işe yaradığını fark ettim (Ne yazık ki)
Bir süredir Rust tarafındaki oyun motorlarını incelemekteyim. Bu konuda sayısız youtube videosu ve öğreti buldum. Hem rust kodlama pratiklerimi geliştirmek hem de meraklı olduğum oyun programlama tekniklerini deneyimlemek için biraz zaman harcadım. Ping Pong oyunundan, uzaydaki göktaşlarını patlatan gemiye, karşısındaki farklı türden blokları onlara top fırlatarak patlatan dikdörtgenden, derin zindanlarda ortografik projeksiyon bazlı kamera kullanan sahalara neredeyse her yerde temel matematikten yararlanıldığına şahit oldum(Öğretilere ait uyguladığım pratikleri ve ortaya çıkan sonuçları game-dev-with-rust reposunda bulabilirsiniz) Bunu zaten biliyordum ama unuttuğum çekirdek matematik bilgim ile yapıldıklarını görünce aslında onlarca yıl önce öğrendiklerimin ne kadar çok işe yaradığını fark ettim (Ne yazık ki)
Oyun sahasına ekranın sağından gelip düz ve çapraz bir çizgide ilerledikten sonra dairesel hareketle devam edip rastgele zamanlarda ateş eden uzay gemisinin kodlamasını öğrenirken ortaya döküken kosinüs ve sinüs çağrıları sonrası ise şöyle bir durup düşünmeye başladım. Devam etmek istiyorsam öncesinde kağıt kalem alıp biraz karalama yapmalıydım. Bugünün popüler oyun motorlarından Unity, Unreal Engine gibilerinin çoğu fizik motorlarından ışıklandırmaya, gölgeleme efektlerinden çarpışma hesaplamalarına, izdüşümsel kamera bazlı 2D sahalardan sıçrama efektlerine kadar pek çok şeyin temel hesaplamasını hazır olarak sunmakta. Hatta IDE desteği sunanlar çok daha öne çıkmakta. Ancak oyun programlamanın temellerinde her zaman olduğu gibi matematik var ve bu atlanmaması gereken bir mevzu(Az biraz cebir fazlasıyla trigonometri)
Oyun platformlarının çoğunda sahne ve nesneler arası ilişkilerde kodlama yapılan yerler oluyor. Bu kısımlar genellikle script diller ile beslenmekte. Ne var ki ister 2D ister 3D olsun vector, normalize, projection, sin, cos, dot, distance, projection, rotate, collision vb kelimeler içeren fonksiyonlara rastlıyoruz. Bunları etkin kullanabilmek için hangi matematik enstrümanlardan yararlandıklarını bilmek gerekiyor. Bu sebeple pek çok oyun motoru dokümantasyonunda temel matematik bilgileri için bölümler var. Benim gibi her şeye sıfırdan başlıyorsanız mutlaka bakmanız gerek.
Bu amaçla öğrendiklerimi her zaman olduğu gibi not almaya başladım. Bu notların hem kendim hem de meraklıları için yararl�� olacağını düşündüm. İzleyen anlatımda temel seviyede oyun geliştirme için bilinmesi gereken matematik enstrümanlara yer verilmekte. Yazının sonunda yer alan kaynakların bu notların oluşmasında büyük bir yeri olduğunu baştan belirtmek isterim. Olaya daha orta okul sıralarından beri bildiğimiz ama teorik kaldığında çok anlamlı gelmeyen bir enstrümanla başlayalım.
Pisagor Teoremi
Oyuncunun roketi iki boyutlu sahada ilerlerken etrafını saran düşman gemileri rastgele yönlerde hareket ediyordu. Bazı düşman gemileri oyuncuya belli mesafe yaklaşınca ateş açıyordu. İşte soru; düşman gemisinin ateş etmek için oyuncuya ne kadar yaklaştığını nasıl buluruz? Problemi basitleştirmek adına oyunun iki boyutlu bir sahada yazıldığını düşünelim. Pek çok oyun motorunda koordinat düzlemi ekranın sol üst köşesini 0,0 başlangıç noktası olarak kabul eder. Bizde böyle olduğunu düşünebiliriz. Tabii 2D kartezyen koordinat sisteminde olduğumuz için işimiz nispeten kolay. Lakin 3D kartezyen sistemine geçtiğimizde sağ el veya sol el kurallarına göre koordinat sisteminin 24 farklı versiyonunun kullanılması söz konusu (2D için bu sayı 8) Şimdilik bu detayları geride bırakalım ve problemimize geri dönelim.
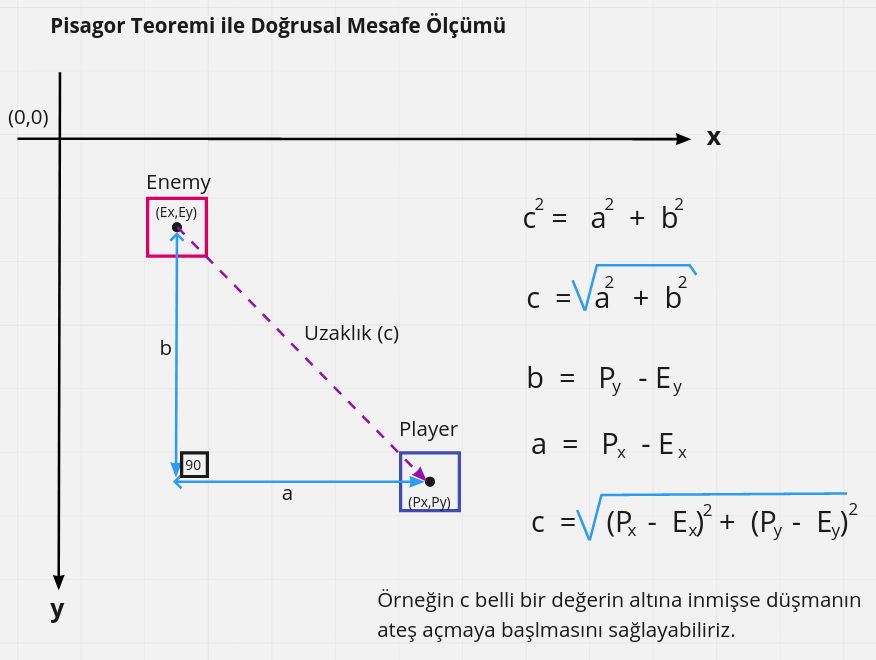
Aslında oyun karakterlerinin(sprite olarak ifade edebiliriz) merkez x,y değerlerini biliyorsak, bir dik üçgenden yararlanarak hipotenüs hesabından hareketle yakınlık değerini bulabiliriz. Bunun nasıl çalıştığını basitçe görmek isterseniz Rust ile yazılmış math101 örneğine bakabilirsiniz. Aşağıda gördülüğü gibi daire, kareye 50 pixel mesafeden daha fazla yaklaştığında ekrana bir uyarı mesajı geliyor.
Vektörler ve Açılar
Oyunlarda vektörler sıklıkla kullanılır. Esasında vektör denilince matematikçiler açısından ilk etapta bir sayı serisi akla gelir. Bu son derece doğaldır. Nitekim V1= [1,2] veya V2 = [3,4,6] ve hatta V3 = [x,y,z,w] gösterimleri birer vektörel ifadedir. Hatta birçok programlama dilinde Vector isimli ve sayısal dizileri işaret eden nesneler bulunur. Lakin oyunlar ve coğrafi özellikleri ön plana çıkınca vektörlerin geometrik anlamı değer kazanır. İki veya üç boyutlu uzaya ait vektörler fazlasıyla kullanılır hatta yeri geldiğinde bu vektörler dördüncü bir boyut olarak zamanı da bünyesine katabilir.
Bir vektör ile büyüklük(daha çok uzunluk olarak da rastlarız) ve belki de en önemlisi yön bilgisi ifade edilebilir. Bu sayede oyun sahasındaki bir nesnenin hareket yönü vektörler ile ifade edilebilir. Büyüklük (Magnitude) yerine yön (direction) bilgisinin önemli olduğu durumlarda ise birim vektör öne çıkar. Bir vektörün uzunluğunu (büyüklüğünü) bulmak için yine pisagor teoremi kullanılabilir. Nitekim uzaydaki bir vektörün uzunluğu iki nokta arasındaki mesafeye tekabül eder ki bu da pisagor üçgeninden yararlanılarak hesap edilir. İşte formüller için özet bir görsel.
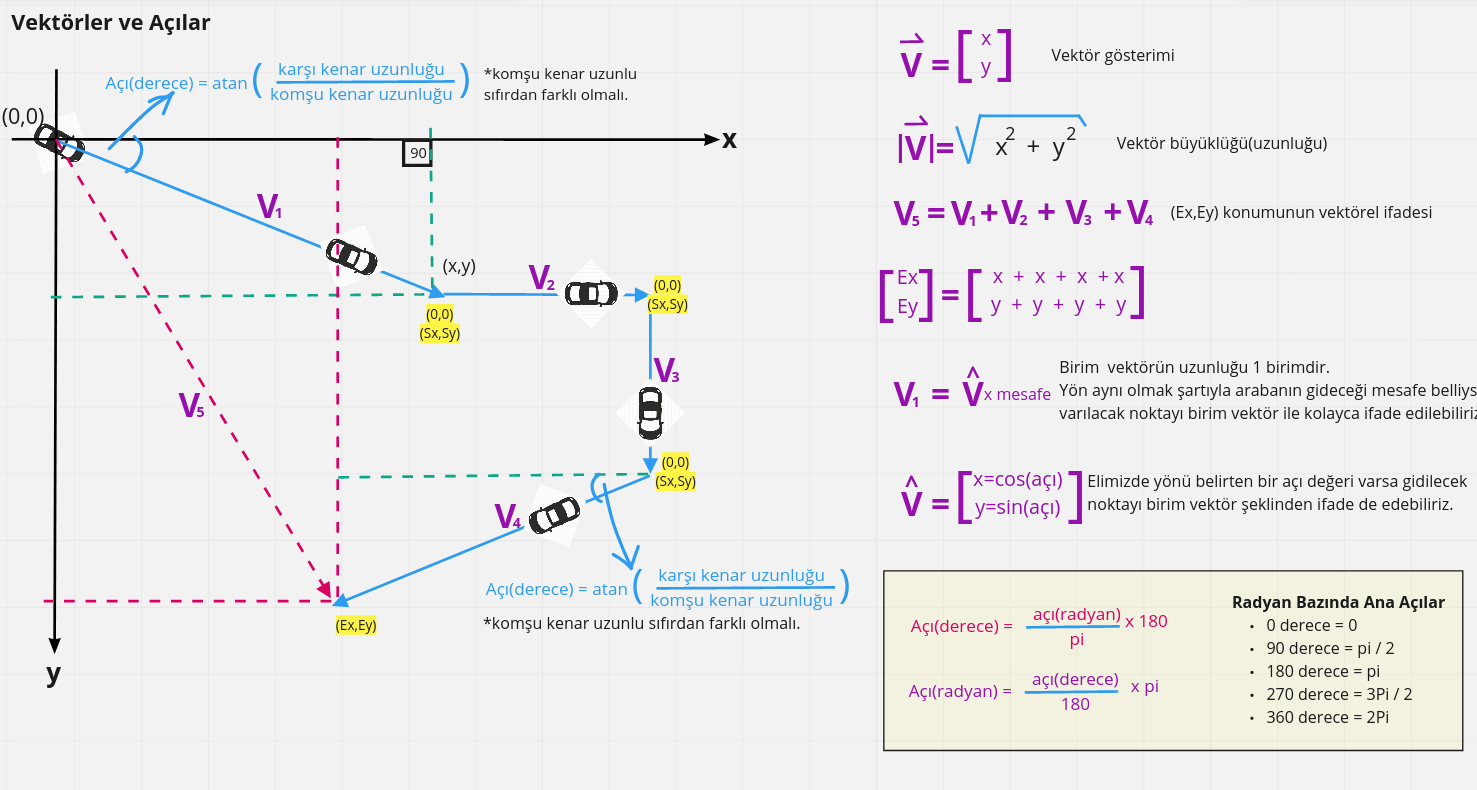
Aslında matematiğin oyun programlama tarafındaki yorumlamaları çok önemlidir. Onları sadece matematiksel formüller veya tanımlar olarak değil fiziki dünyada anlamlandırılan birer enstrüman olarak düşünmek lazım. Bu anlamda üstteki grafiği biraz yorumlamaya çalışalım. Aracın son konumunu merkez kooridnatlara göre Ex ve Ey ile ifade edebiliriz. Ancak merkezden (Ex,Ey) konumuna olan uzaklık vektörel olarak da ifade edilebilir. (Ex,Ey)'yi vektör olarak düşündüğümüzde şöyle bir paragraf düşünebiliriz. Oyuncunun kullandığı araba güney doğu yönünde 4 birim ilerledikten sonra doğuya doğru 2 birim ardından güneye 2.5 birim ve son olarak da güney batıya doğru 3 birim hareket etmektedir. Dikkat edileceği üzere burada koordinatlar belli değildir. Sadece bir yer değiştirme hareketi söz konusudur(Displacement) Bir başka deyişle vektörler aslında nesnelerin yer değiştirmeleri ile sıkı bir şekilde ilgilenir. Bu nedenle (Ex,Ey)'nin standart olarak x,y cinsinden merkeze uzaklığının ifadesinden farklı bir anlam taşır. Başka bir örnek verelim; Gemimiz kuzey yönünde saatte 340 km hızlar ilerliyor. Burada dikkat edileceği üzere herhangi bir uzay koordinatı bilgisi yoktur. Hatta konum bilgisi tamamen göreceli bir olgu haline gelmiştir. Konum Lizbon limanına göre farklı, oyuncunun baktığı ekrana göre farklı ve hatta güneşin konumuna göre dahi farklıdır. Vektörel olarak ifadesi ile aslında yönü ve büyüklüğü(ki burada hız oluyor) anlatılmaktadır.
Bu sebeplerden vektörler sayesinde bir noktanın merkeze olan uzaklığını ifade etmek de kolaydır. Örneğin görseldeki araba her yön değiştirdiğinde gittiği mesafeyi büyüklük olarak kabul eden ve bir yönü olan vektörler ile matematiksel olarak ifade edilebilir. Buna göre aracın son geldiği (Ex,Ey) noktasının vektörel formdaki karşılığını bulmak kolaydır. Ayrıca (Ex,Ey) noktasının vektörel ifadesi arabanın merkezden(merkez olarak başka bir nesne konumu örneğin yol kenarındaki bariyer de kabul edilebilir) ne kadar uzakta olduğunu söyler. Lakin az önce belirttiğimiz üzere özellikle iki boyutlu saha kullanan oyunlarda vektörün büyüklüğü(uzunluğu) göz ardı edilebilir. Yön(direction) daha önemli ise. Bu sebeple birim vektöre(Unit Vector) sıklıkla rastlanır. Herhangi bir vektörü normalleştirme(normalizing) işlemine tabi tutarak birim vektör cinsinden ifade etmek mümkündür.
Yukarıdaki görselde yer alan senaryonun cebirsel ifadesini düşündüğümüzde V5 vektörünün diğer vektörlerin toplamı olarak ifade edilebileceğini de söyleyebiliriz. Burada üçgen kuralı(Triangle Rule) kullanılmaktadır ve V5 = V1 + V2 + V3 + V4 eşitliği geçerlidir. Bir başka deyişle başlangıç noktasından itibaren yön değiştirerek ilerleyen bir aracın son konumunu ifade eden bir vektör tanımına ulaşabiliriz. Buradan hareketle birim vektöre dönüşütürüp göreceli olarak başka şeylerle kıyaslayabilir, ilersinde mi gerisinde mi ters yönde mi aynı yönde mi gibi sonuçlara da varabiliriz.
Vektörlerde 0,0 konumuna göre kurulan dik üçgenlerden yararlanılarak yönü belirten açılar da kolaylıkla hesaplanabilir. Genelde bu hesaplamalar dik üçgenin karşıt kenarı ile komşu kenar arasındaki oranın arktanjantı şeklinde hesaplanır(tanjantının -1 üssü yani kotanjant değeridir esasında) ve derece cinsinden bulunur. Oyun motorlarının çoğunda derece yerine radyan kullanılır. Bir daireyi dört eşit dilim olarak böldüğümüzde radyan ile dilimlerin pi değeri cinsinden ifade edilmesi sağlanır. Bulunan açının radyana çevrilmesi ya da tam tersinin yapılması da formüller ile mümkündür.
Yön için önem arz eden açının bulunmasında sadece tanjant değil zaman zaman sinüs ve kosinüs fonksiyonları da kullanılabilir. Aslında varmak istediğim nokta biraz da şu. Elimizde radyan cinsinden açı ve örneğin bir kenar bilgisi varsa oluşan dik üçgenin diğer kenarını hesap etmek, başka bir deyişle hedef x,y koordinatlarına ulaşmak kolaydır. Buna göre,
- Elimizde açının karşı kenar uzunluğu ile hipotenüs değeri varsa sinüs fonksiyonundan yararlanılarak açı bulunabilir.
- Elimizde bulunmak istenen açının karşıt kenar uzunluğu ile komşu kenar uzunluğu varsa tanjant fonksiyonundan yararlanılır.
- Son olarak elimizde bulunmak istenen açının komşu kenar uzunluğu ile hipotenüs değeri varsa kosinüs fonksiyonundan yararlanılabilir.
Bu noktada açı ile vektör arasındaki ilişkiyi ve dolayısıyla bir vektörün yönünü bulmayı iyi anlamak gerekir. Elimizde bir açı varsa birim vektör cinsinden yönü bulmak oldukça kolaydır. Buna göre açının sinüsü y değerini, kosinüsü de x değerini bulmamızı sağlar. Araştırmalarıma göre açı bilgisine sahip olduğumuz durumlarda x,y değerlerinden hangisinin kosinüs hangisinin sinüs ile hesaplanacağını alfabetik sıralamalardan bulabiliriz. Alfabetik sıralarına göre x, y'den önce geldiği için cos'da sin'den önce gelmelidir... Sanırım ne demek istediğimi anladınız :)
Gelin bir sinüs eğrisinin kullanıldığı örnek kod parçasının çalışmasına bakalım. Sol ve sağ ok tuşlarına basıldığında dairenin x kooridanatı değerine göre sinüs değeri hesaplanır ve y değeri buna göre değiştirilir. Sonuçta altın renkli topun sinüs eğrisine göre hareketi söz konusudur. Tabi normalde sinüs eğrisine baktığımızda ilk hareketin yukarı yönlü başladığını görürüz. Ancak burada koordinat sisteminde 0,0 orjininin ekranın sol üst köşesinde olduğunu hatırlayalım. Yine de y değerinin artım ve azaltımını duruma göre değiştirip aşağı ve yukarı yönlü hareketleri kontrol edebileceğimizi unutmayalım. Tabii bu söylediğim kanun hükmünde kararname değildir ve bu kadar katı düşünmeye gerekte yoktur. Çünkü;
Oyun sahası oyuncunun hakimiyetindedir ve oyun programlamada altın bir kuraldan bahsedilir. Doğru görünüyorsa doğrudur (If it looks right, it is right - 3D Math Primer for Graphics and Game Development, Fletcher Dunn)
Nokta Çarpım(Dot Product)
İki boyutlu oyun sahasında nesnelerin yönleri arasındaki açının değerlendirildiği pek çok durum var. Örneğin bir uçağın bir checkpoint noktasından geçip geçmediğini anlarken ya da karakterin yokuş aşağıya indiğini veya yukarı doğru çıktığını hesaplarken açıları kullanabiliriz. Aşağıdaki gösterimde uçağın yönü ile checkpoint noktasının yönü arasındaki ilişkinin nokta çarpım ile ele alınışı değerlendirilmekte. Bu senaryolarda birim vektörlerin göz önüne alındığını baştan belirteyim. Nitekim buradaki senaryoda vektörün büyüklüğünden ziyade yönü önemli. Birim vektör cinsinden bir nesnenin yönünü ifade ettiğimizde aradaki açıyı bulmak için nokta çarpımı formülasyonundan da yararlanabiliyor. Nokta çarpım hesaplaması ters tanjant ya da ters kosinüs ile bulunan açı hesaplamasına göre işlemciye daha az yük bindirmekte. Yani işlem maliyeti çok daha ucuz. Bu sebeple pek çok oyun motoru bu fonksiyonelliği hazır olarak da sunmakta.
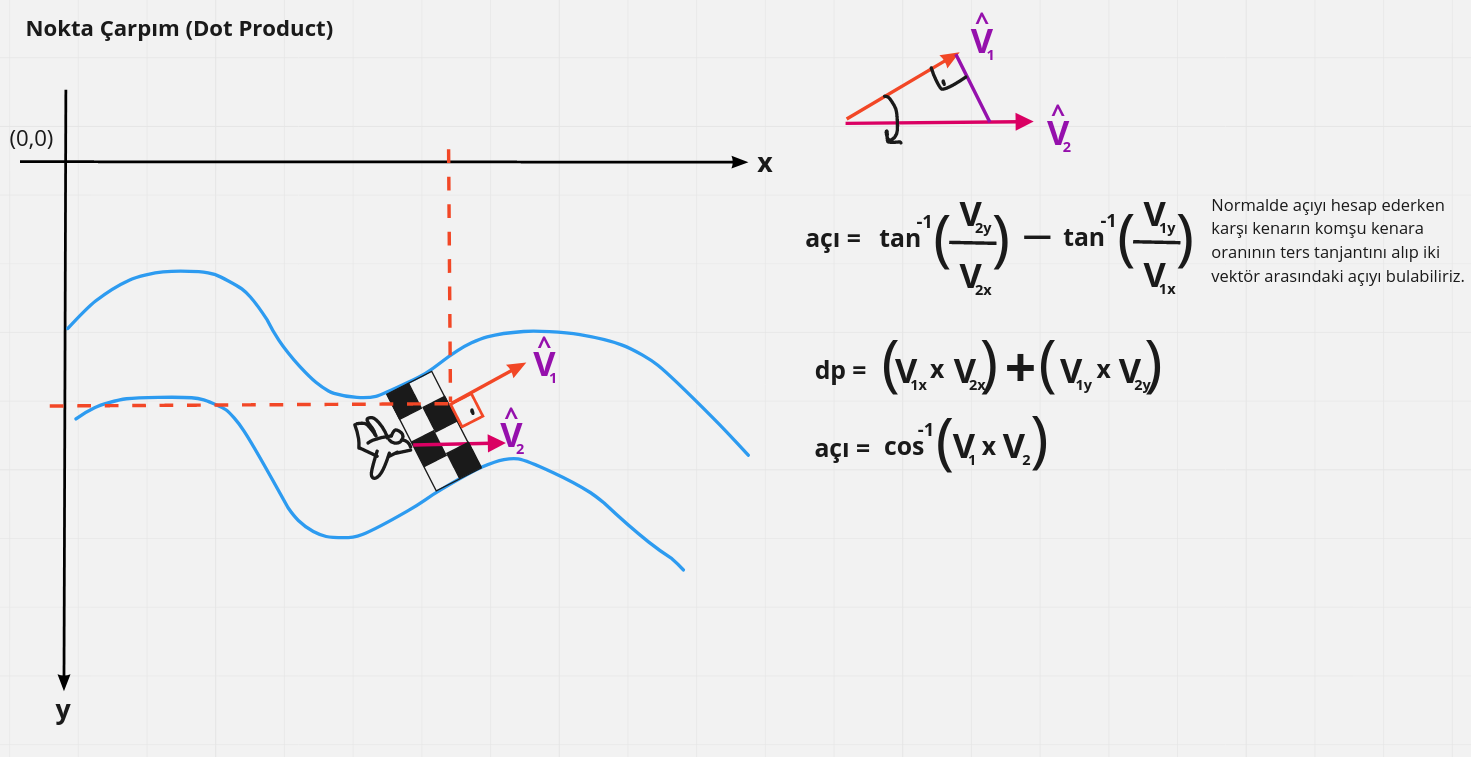
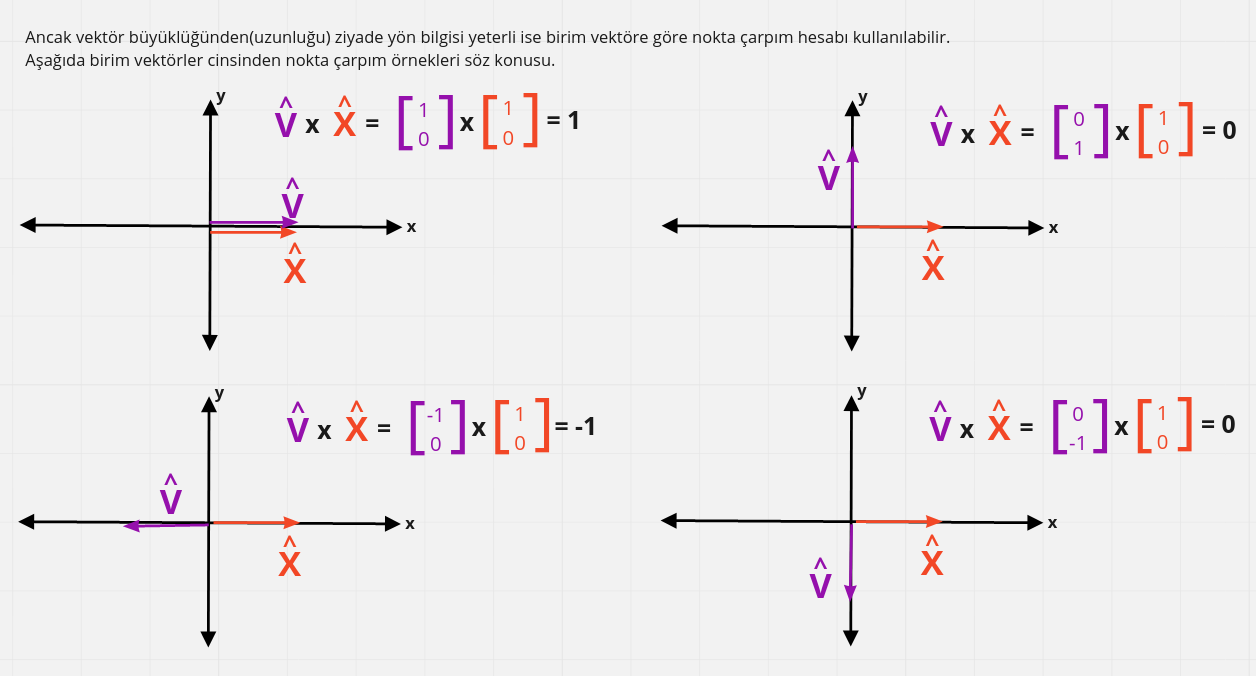
Nokta çarpımını birim vektöre indirgediğimizde elde edilen skalar değer -1 ile 1 aralığında olacaktır. Buna göre vektörlerin aynı veya ters yönde olduklarını ya da birbirlerine yaklaştıklarını veya uzaklaştıklarını anlayabiliriz. Yani açısal olarak anlamlandırdığımızda dar veya geniş açıların farkındalığına göre bir karar verebiliriz. Aşağıdaki görselde birim vektörlerin konumlarına göre uç nokta değerleri görülmektedir. Şimdi size kendi başınıza bir çalışma önerisinde bulunayım. Sağ vektörün bitiş noktasından tekrar kendisine gelecek şekilde bir çember çizin. Çemberin ana kartezyen doğruları ile kesim noktalarını pi cinsinden ifade etmeye çalışın. Ardından çember üstündeki herhangi bir noktanın x,y koordinat değerlerini trigonometrik fonksiyonları kullanarak bulmayı deneyin. İşte bir çember yörüngesinde hareket ettirmek istediğiniz uzay gemisi için gerekli hesaplamaların temel matematiğini keşfettiniz.
Skaler İzdüşüm (Scalar Projection)
Vektörler arası nokta çarpım operasyonunun bir kullanım şekli de skaler izdüşüm değerinin bulunmasıdır. Esasında bu değer yardımıyla örneğin bir yarışta önümüzdeki aracın ne kadar mesafe gerisinde olduğumuzu hesaplamak için bu enstrümandan yararlanabiliriz. Ancak bu senaryoda vektörlerden birisi birim vektöre indirgenir(Normalizasyon) ardından diğer vektör ile nokta çarpım işlemine tabii tutulur. Elde edilen sonucun işareti(pozitif veya negatif olması) yönü de ifade eder ama daha da önemlisi aradaki mesafe farkını öğreniriz. Burada izdüşümsel bir tespit söz konusudur. Aşağıdaki grafikte durum biraz daha net anlaşılabilir.
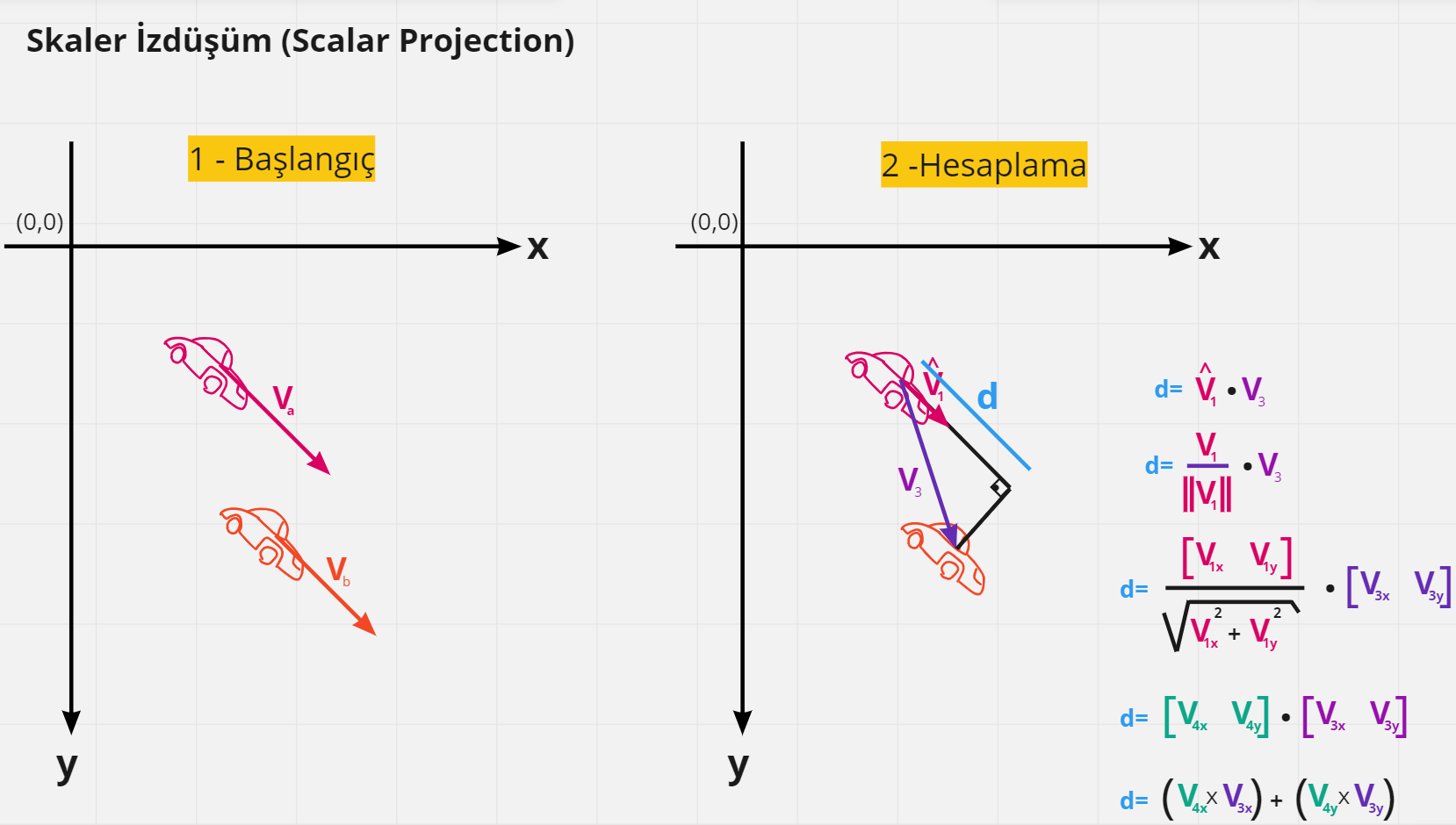
İki boyutlu koordinat sistemimize göre güney doğu yönünde hareket eden iki yarış arabası var. Arkadaki aracın öndekinden ne kadar mesafe geride olduğunu bulmak istiyoruz. Öncelikle ilk aracın yönünü ifade eden vektörü(Va) birim vektöre çevireceğiz(V1). Ardından elde edilen vektörü şekilde çizilen ikinci vektör ile(V3) ile nokta çarpım işlemine tabii tutacağız. Birim vektöre çevirme işlemi(normalizasyon) bilindiği üzere vektörün kendisinin, büyüklüğüne oranı ile hesap ediliyor. Buradan elde edeceğimiz vektörü örnekte(V4) olarak isimlendirdik. Geometrik olarak düşünürsek yaptığımız işlem V3 vektörünün V1 birim vektörü üstünden geçen hayali doğrudaki izdüşümünü bulmak. Dikkat edileceği üzere izdüşümü oluşan dik üçgenin V1 vektör düzlemindeki kenarına karşılık geliyor. Böylece aynı paraleldeki bu iki araba arasındaki mesafeyi A aracına göre hesap etmiş olduk(A aracına göre dedim dikkat ederseniz) Konuyu pekiştirmek adına bir antrenman sorusu üstünde düşünelim. B aracının yönünü işaret eden vektörü birim vektöre dönüştürüp, B'dan A aracına çizilen yeni bir vektör ile nokta çarpım işlemine tabii tutsaydık aynı mesafe değerini bulur muyduk ve bulursak işareti negatif mi yoksa pozitif mi olurdu?
Nokta çarpımı ve birim vektör ilişkisi ile ilgili olarak şu özeti de geçebiliriz. İki birim vektöre arasındaki açıyı bulmak için nokta çarpımların ters kosinüsü(arkkosinüs) fonksiyonundan yararlanılabilir. Aradaki açıyı bulmak için birim vektör kullanmak zorunda da değiliz. Nitekim iki vektörün nokta çarpımı büyüklükleri ile aradaki açının kosinüs değerinin çarpımına eşittir. Buradan yola çıkarak iki vektörün nokta çarpımının, vektör büyüklüklerinin çarpımına olan oranının arkkosinüs değeri bize yine aradaki açıyı verecektir.

Doğrusal İnterpolasyon(Linear Interpolation)
Oyun sahasında başvurulan matematik enstrümanlarından bir diğeri de Linear Interpolation kavramıdır. Örneğin motion efektlerinde, belli bir rotayı izlemesi istenen unsurlarda, renk geçişlerinde, giderek hızlanan veya yavaşlayan nesnelerde sıklıkla başvurulur. En basit formu da iki nokta arasında gidilmesi istenen mesafenin zamansal olarak kesin bilindiği hareket efektleridir. Örneklendirirsek daha iyi olacak. Diyelim ki 2D kartezyen sisteminde x,y değerlerini bildiğimiz A ve B noktaları var. Diğer yandan oyun nesnesinin A noktasından B noktasına tam tamına 10 saniyede varacağını planlıyoruz. Amacımız herhangi bir t anında bu nesnenin iki nokta arasındaki doğruda hangi x,y koordinatlarında olduğunu öğrenmek ki buna göre onun otomatik hareketlenmesini sağlamamız mümkün olur. Aşağıdaki grafikte bu hesaplama için kullanılabilecek formüllere yer veriliyor.
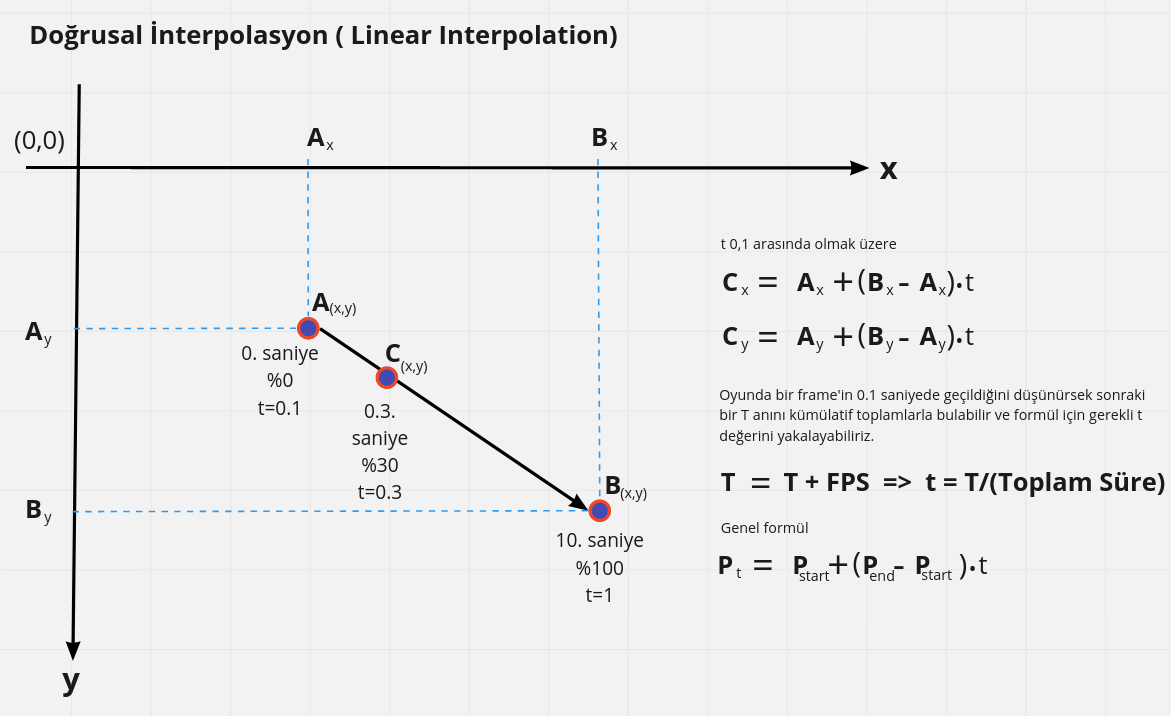
Başlangıç aşamasında A konumunda olan nesnenin 10ncu saniyede B konumunda olacağını biliyoruz. Buna göre örneğin C konumundan geçerken mevcut x,y koordinatlarını bulmak istersek nasıl bir formül kullanırız? Esasında zaman çizelgesini yüzdesel olarak ifade edersek işimiz çok daha kolaylaşıyor. Başlangıç konumu olasılığı %0 hali ile ifade edilirse 10ncu saniyede varış noktasına gelmiş olmamız da %100'e karşılık gelir. Yani varış noktasında isek nesne yüzde yüz kesinlikte rotasını tamamlamıştır. Bir başka deyişle başlangıç ve bitiş noktalarını yüzdesel olarak düşündüğümüzde 0 ile 1 arasında yer alan bir olasılık değerinden bahsedebiliriz. Bu değer formülümüzdeki t parametresine karşılık gelir ve oyunda kullanılan FPS(frame per second) bilgisine göre ayarlanır. Örneğin her bir frame 0.1 saniyede geçiliyorsa bir T anını T = T + 0.1 gibi ifade edebiliriz. Kendi senaryomuzda bu T değerinin 10'a bölümü hesaplamadaki t değerini verecektir. Bir başka deyişle elimizde FPS değeri varsa herhangi bir andaki t değerini hesaplamak kolaydır.
İşin zorlaştığı noktalardan bir tanesi yerçekiminin devreye girdiği ya da rotanın doğrusal olarak ifade edilemediği eğrilerden oluşan senaryolardır. Örneğin önündeki tepeden space tuşuna basınca sıçyarak karşı tepeye ulaşmaya çalışan bir arabayı göz önüne alalım. Böyle bir durumda yerçekimine göre bir eğri çizilmesi ve bunun zaman bağımlı olarak hesaplanması gerekir. Bu senaryo için aşağıdaki şekli göz önüne alabiliriz. Hareket halindeki aracın bulunduğu noktayı bir vektör olarak ifade edeceğiz(P ile ifade edilen kısım) Ayrıca t anında gittiği yönü taşıyan birde hız vektörü kullanmaktayız(V ile ifade edilen) t ile oyun motorlarının bize genellikle hazır olarak verdiği delta time değerini ifade ediyoruz. Nitekim oyuncunun oynadığı platform ne olursa olsun herkesin aynı süresel değeri kullanması önemli. Çok oyunculu çevrimiçi platformlarda da FPS farklılıklarını ortadan kaldıracak bir özellik diyebiliriz sanırım.
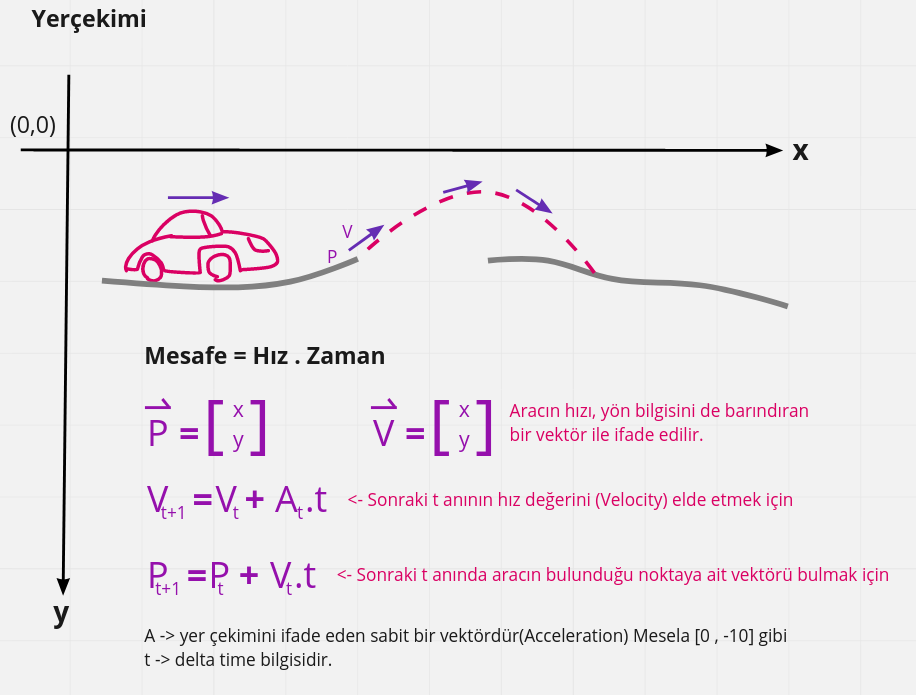
Aracın t+1 anındaki konumunu ifade eden vektörü bulmak için hız vektörü ile delta time bilgisinin yer aldığı bir formül kullanılır. Ancak öncesinde o anki hız değerini işaret eden vektörün yine delta time ve yer çekimi vektörünün hesaba katılacağı bir formül ile bulunması gerekir. A ile ifade edilen(genelde Acceleration olarak bilinir) vektör bu senaryoda yerçekimini işaret eden sabit bir vektör değeridir.
Birim Çember ve Dairesel Hareket
Az önce kartezyen üzerindeki bir oyun nesnesine dairsel bir rotada hareket vermek istersek x,y koordinatlarını nasıl hesap edebileceğimizi sormuştuk. Esasında bazı oyun nesnelerinde çemberin büyüklüğünden ziyade merkez koordinatlarına göre hangi yöne gideceğinin belirlenmesinde birim çemberi baz alan vektörlere sıklıkla başvurulduğu görülüyor. Aşağıdaki grafikle durumu biraz daha iyi anlayabiliriz.
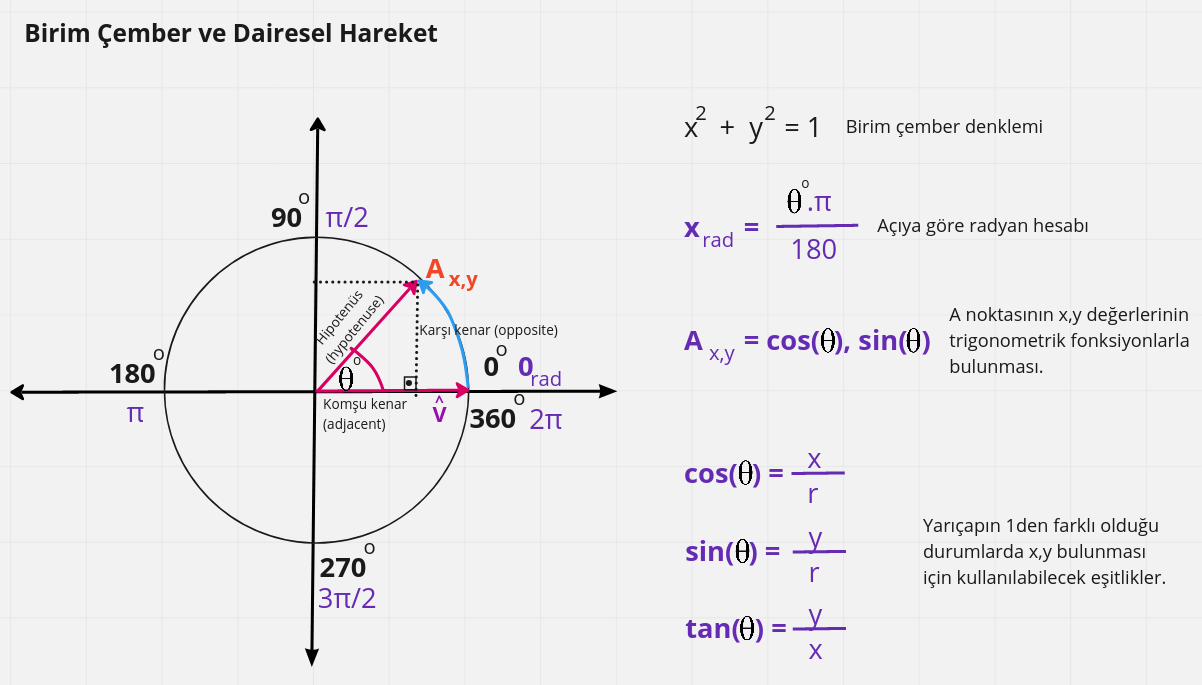
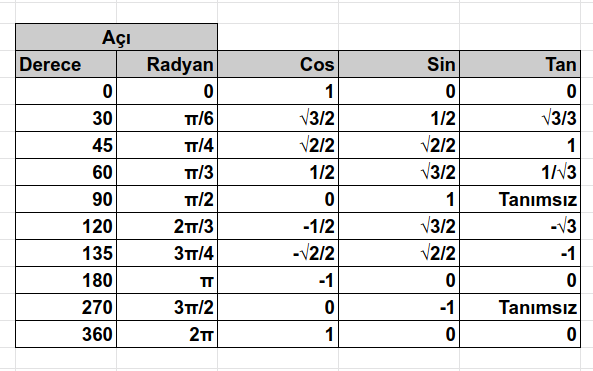
Çemberin yarıçapının birim vektör olduğunu kabul edelim. Bu yüzden çemberimiz de birim çember olarak ifade edilir. Buna göre 0° açıya göre konuşlanan bir vektörün θ(teta) açısı kadar saat yönünün tersine doğru hareket etmesi, çemberin yarıçapı kadar olan bir yörüngede belli bir mesafe yol kat edilmesi anlamına gelir. İşte bu kat edilen mesafeyi radyan cinsinden ifade edebiliriz. Hatta gösterimde çember eğrisi üstündeki rotada bir hareket söz konusudur. Bu hareketi cebimize koyalım ve v = [1,0] vektörüne göre oluşan açı değişimi için de bir şeyler söyleyelim. Genelde halk arasında açılar hep derece cinsinden ele alınır lakin matematikçiler açı yerine daha çok radyan birimini kullanmayı tercih ederler. Nitekim bir çember ile tarif edilen ve 0° ile 360° arasında değişen açıları 𝜋(pi) cinsinden tanımlamak ve buna göre çember üstünde kat edilen mesafeyi de 𝜋 değerlerine göre ifade etmek mümkündür. Söz gelimi 0°, 0 radyan iken tam tur yani 360° bir dönüş 2𝜋 değeri ile ifade edilebilir. Buradan yola çıkarak bir radyanın 180°/𝜋 ile ifade edilebileceğini görebiliriz. Diğer yandan bilinmeyen bir radyan değeri için görseldeki formülden yararlanılabilir. Aşağıdaki tabloda bazı popüler açıların derece, radyan, kosinüs, sinüs ve tanjant tringonometrik fonksiyonları cinsinden değerlerine yer verilmektedir.
Çember üstündeki harekete ait dikkat edeceğimiz önemli noktalardan birisi de aslında x,y koordinatları için hep bir dik üçgenin çizilebilecek olmasıdır. Pozitif x ekseni üstündeki birim vektörün büyüklüğünün çember hareketi sırasında 1 ile -1 arasında hareket ettiğini fark etmiş olmalısınız. Buna karşın çember üstündeki vektörün merkeze olan mesafesi sürekli olarak dik üçgenin durumuna göre değişmektedir. x ve y değerlerinin bu dik üçgene göre pisagor teoremini kullanarak hesaplanması da oldukça kolaydır. Hipotenüsün de aslında bir vektör olarak ifade edilebileceğini belirtelim. Ele aldığımız senaryoda [1,0] birim vektörümüz ve açı bilinmekte. Dolayısıyla trigonometrik fonksiyonlar yardımıyla x,y değerlerini hesaplayabilir ve dairesel hareketin tüm noktalarını gezebiliriz. Peki tüm bunlar ne anlama geliyor? Eğer yarıçapını bildiğimiz bir çember varsa açıyı 0 ile 2𝜋 arasında dolaştırarak x ve y değerlerini bulabiliriz. x değeri açının kosinüsünün yarıçap ile çarpımına, y ise açının sinüsünün yarıçap ile çarpımına eşit olacaktır. Aşağıdaki animasyonda yine rust ile yazdığımız örnekte oluşan sonucu görebilirsiniz. Space tuşuna basınca kahverengi daire dairesel bir hareket gerçekleştirmektedir.
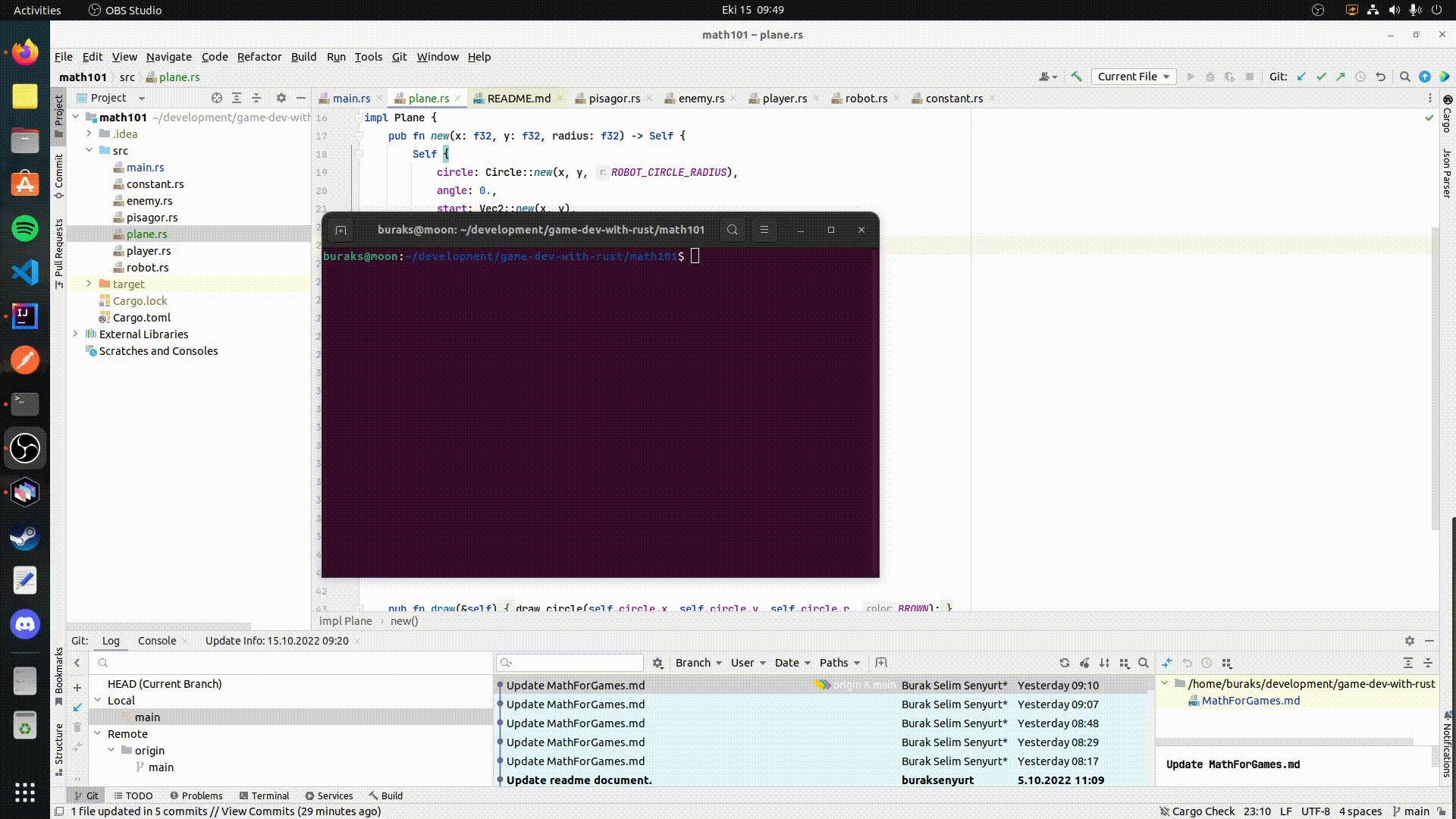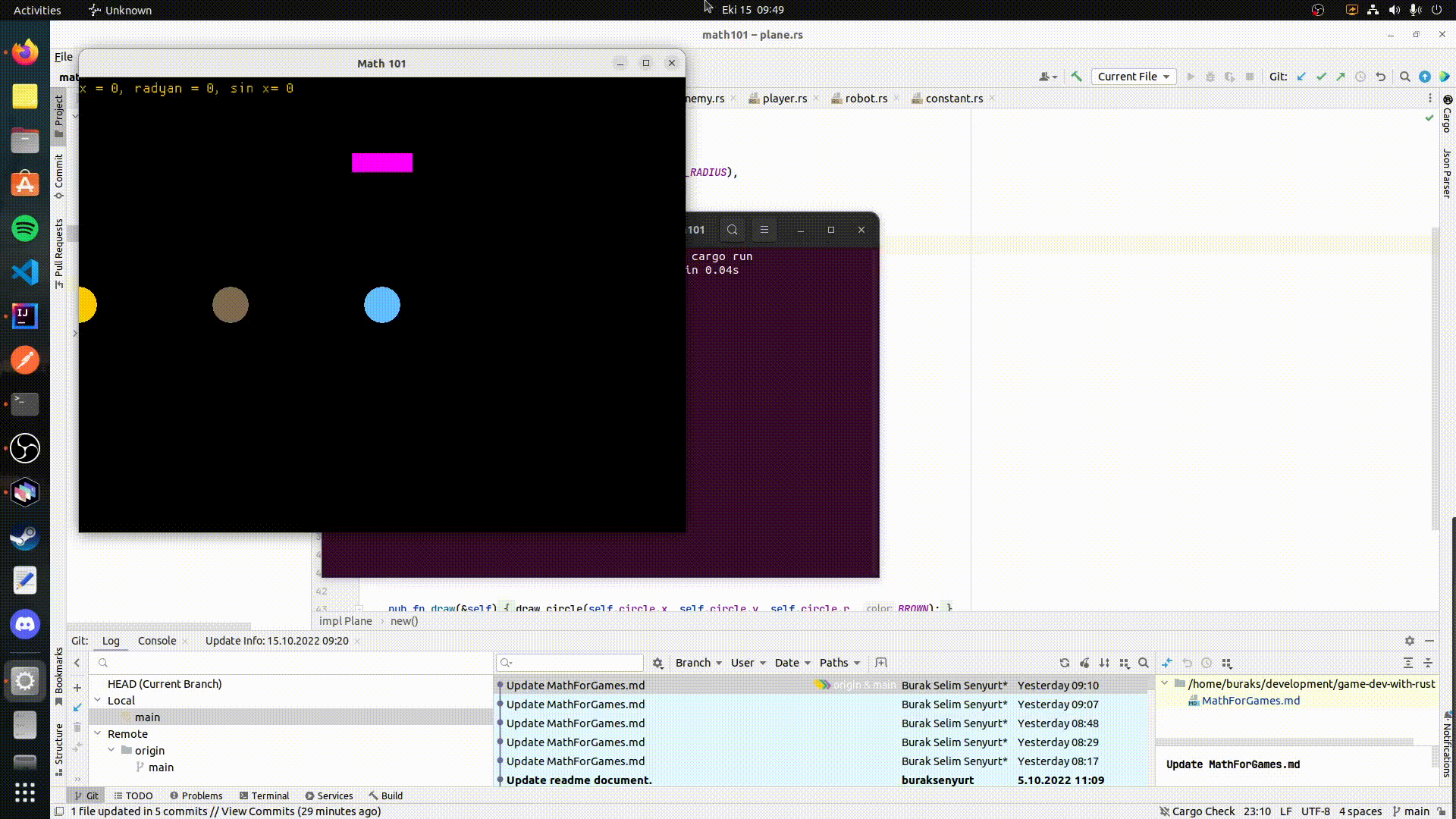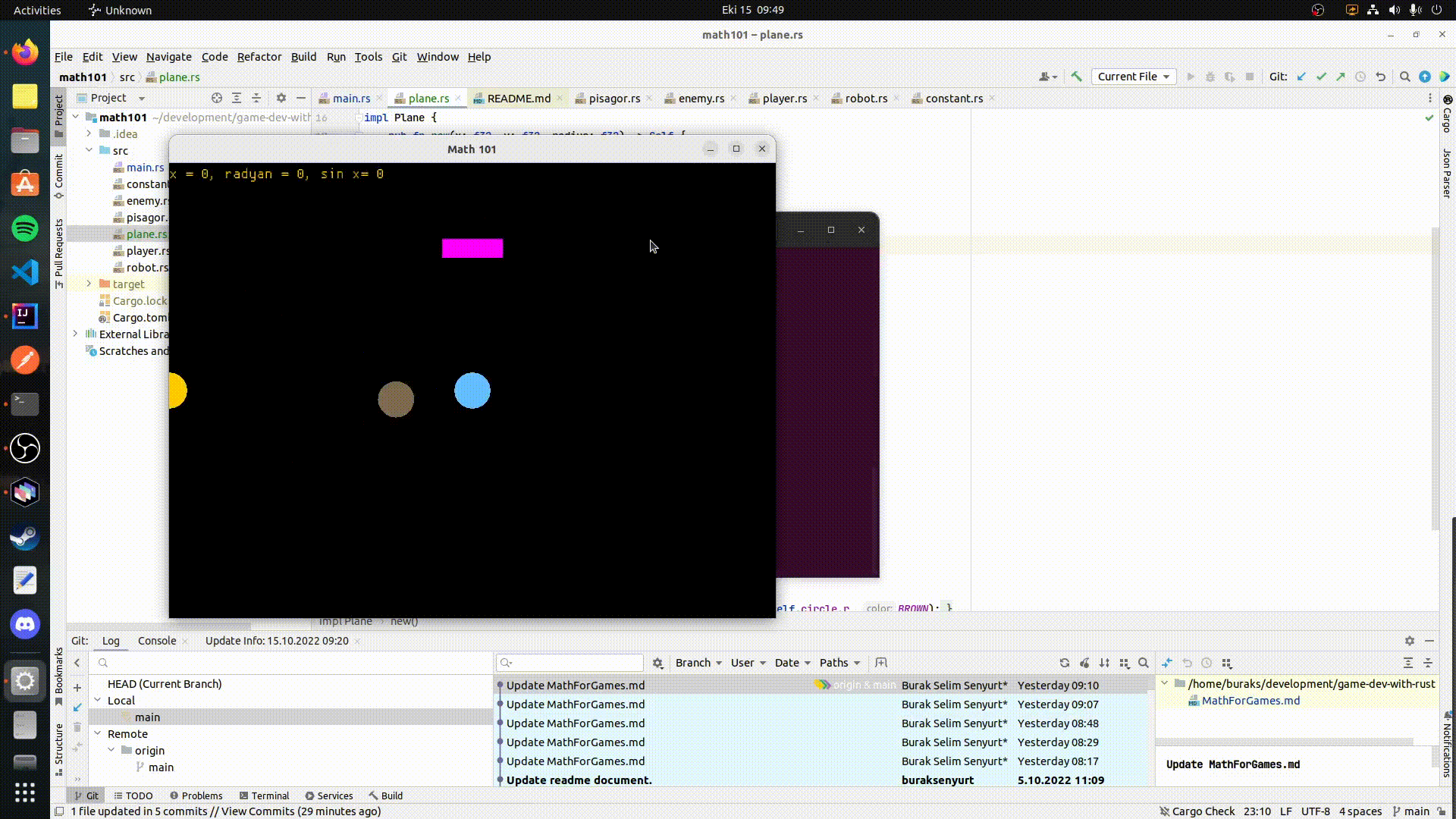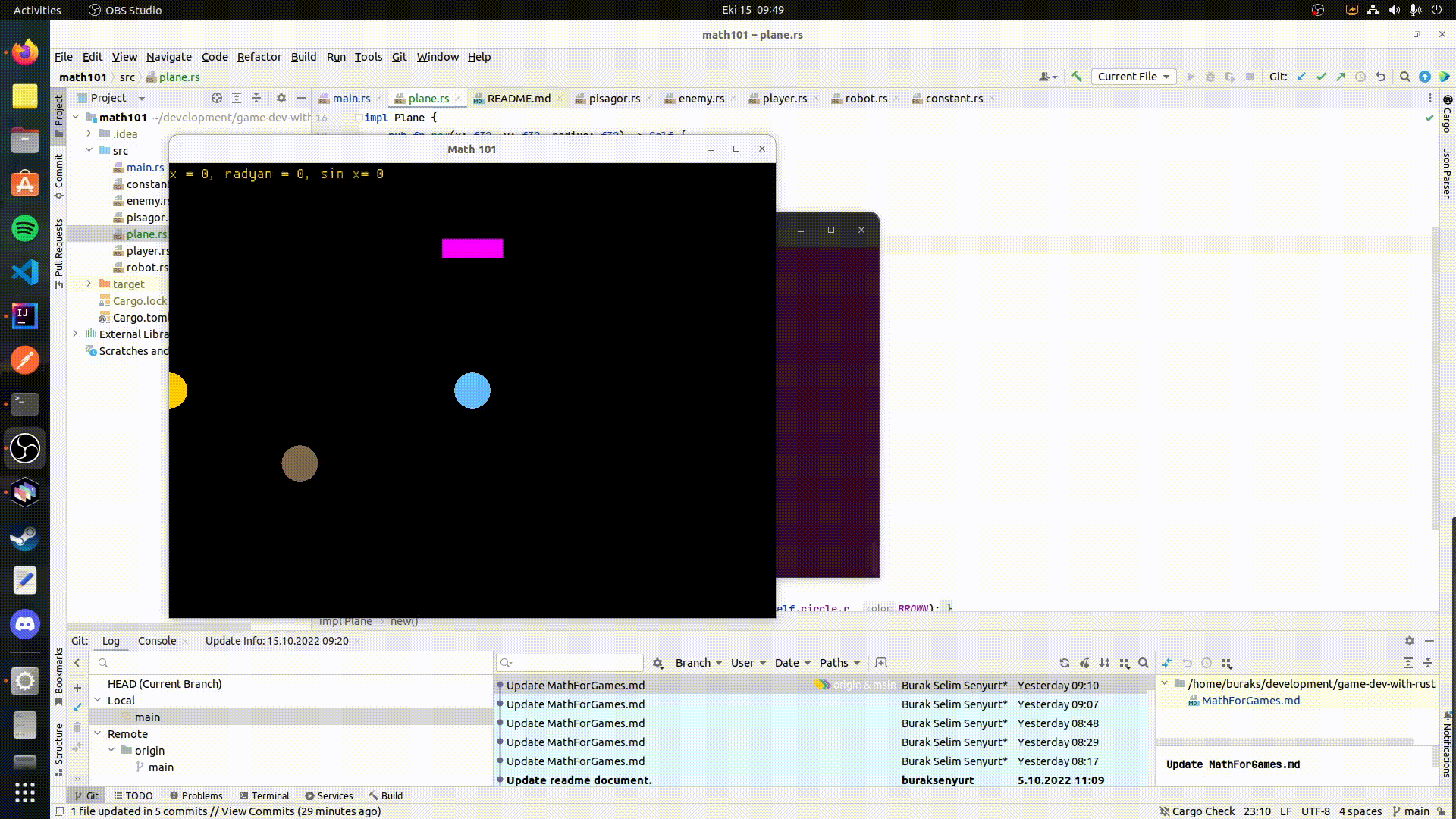
Bu örneklerden yola çıkarak size tavsiyem hakim olduğunuz programlama dilini kullanarak bir eliptik yörünge hareketini uygulamaya çalışmanız olacaktır.
Elbette oyun geliştirmede kullanılan matematiksel enstrümanlar bunlarla sınırlı değil. Matrisler, lineer cebir gibi daha bir çok konu başlığı bulunmakta. İlerleyen zamanlarda bu konulara da değinmek istiyorum. Yine de basit oyun kinematiği üzerine gerekli denklemlerin üzerinden geçtiğimizi söyleyebilirim. Sadece vektör ve açıları kullanarak bile sahadaki karakterleri yönlendirmek, hızlandırmak, bir yerlere çarpıp çarpmadığını bulmak kolaydır. Fakat unutulmaması gereken bir husus var; Aynı sonuca varmak için farklı denklemler kullanılabilir ve bazıları işlemciyi daha az yoracak türden olabilir.
Tabii tüm bu teroik bilgileri bir şekilde denemek de gerekiyor. Ben biraz daha zor olan yolu seçip Rust tarafındaki oyun motorlarından faydalanmaya çalıştım. Nitekim Unity, Unreal Engine gibi zengin IDE desteğine sahip platformlarda bu matematik bilgilerine ihtiyaç duyulmayabilir. Görsel geliştirme ortamları çoğunlukla sürükle bırak yöntemi ile birçok şeyin üstesinden geliyor. Rotayı çiziyor, süreleri veriyorsunuz ve ta taaa... Yabancı gemi o formasyonda hareket ediveriyor. Siz yine de asıl dinamikleri öğrenmeye bakın. Böylece geldik bir maceranın daha sonuna. Bir başka yazıda buluşmak üzere hepinize mutlu günler dilerim.
Özet Çevirinin Hazırlanmasında Yararlandığım Kaynaklar