Merhaba Arkadaşlar,

Uzun zamandır algoritmalar üzerinde çalışmadığımı fark ettim. İşlerin biraz olsun hafiflediği şu vakitlerde de bir tanesini inceleyeyim dedim. Derken kendimi Floyd-Warshall algoritmasını anlamaya çalışırken buldum. Söz konusu algoritma Graph yapılarında boğumlar arasındaki en kısa yolların bulunmasında kullanılmaktadır.

Gerçek hayat örnekleri düşünüldüğünde Regular Expression, Network Routing, Dynamic Programming, yönsüz graph'ların iki parçalı graph'lar dönüştürülmesi ve daha bir çok alanda kullanıldığına şahit oluruz. Algoritmanın matematiksel çalışmasına bakıldığında boğumların birbirlerine olan yakınlıklarını ele alan matrisleri kullandığını görürüz.

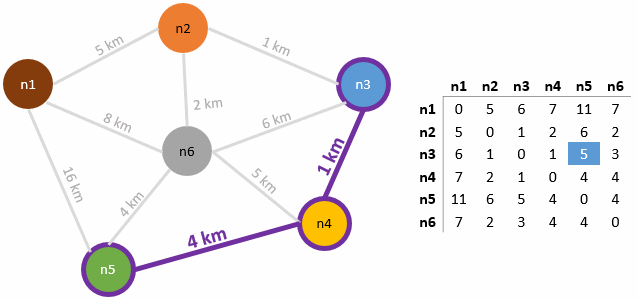
Aslında konuyu eğlenceli olabileceğini düşündüğüm bir senaryo üzerinden ele alırsak çok daha iyi olur. Bu anlamda aşağıdaki grafiği göz önüne alalım. (Grafiğin oluşmasında Quora'nın bana çok güzel fikir verdiğini ifade etmek isterim)

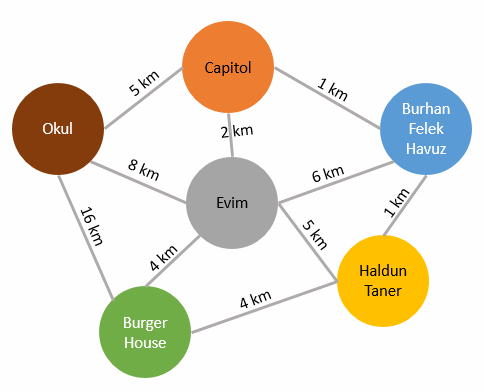
Biz evimizde oturuyoruz ve örneğin Haldun Taner sahnesine gideceğiz. Normal şartlarda direkt bir güzergah kullanırsak 5 km yol gitmemiz gerekiyor. Diğer yandan önce Capitol'e, oradan Burhan Felek'e ve oradan'da Haldun Taner'e geçersek toplamda 4 km yol katediyoruz. 1 km kazancımız var bu güzergahı takip edersek. Eğer önce Burhan Felek'e oradan Haldun Taner'e geçersek de 7 km yol kat edeceğiz. Senaryoyu biraz daha geliştirelim. Diyelim ki evden Burger House'a gideceğiz. Karnımız acıkmış. Doğrudan gidersek 4 km yol almamız lazım. Farklı güzergahlar da tercih edebiliriz. Örneğin Haldun Taner üzerinden geçersek 9km, Okul üzerinden geçersek 24km yol. Bunun gibi bir yerden diğer bir yere giderken pek çok güzergah ve mesafe belirlenebilir.

İşte Floyd-Warshall algoritması bir boğumdan diğer bir boğuma gitmek için kullanılabilecek en kısa yolların çıkartılmasında devreye girerek karar vermemizi kolaylaştırır. Şimdi yukarıdaki senaryoyu biraz daha bilimsel hale getirip lokasyonlar arasındaki en kısa mesafeleri bulmaya çalışalım. Öncelikle boğumlarımıza aşağıdaki gibi numaralar verelim ve ilk olarak yakınlık matrisimizi oluşturalım. (Yakınlık matrisinin ilk versiyonu boğumların komşu boğumlar ile arasındaki mesafelerini tanımlamaktadır)

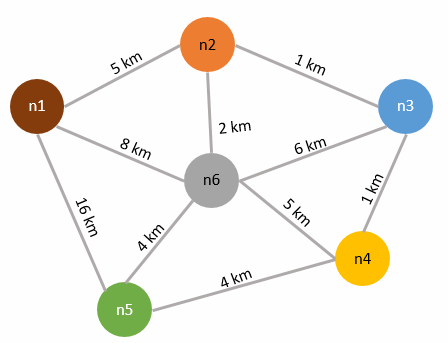
Matrisimizin ilk hali aşağıdaki gibi olacaktır.

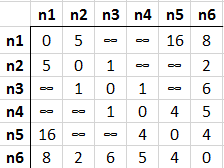
Bu matris bize ne söylüyor acaba?

Bazı hücrelerde sonsuzluk sembolü, bazı hücrelerde ise sıfır değeri var. İki boyutlu bu matris boğumların en yakın diğer boğuma olan mesafelerini göstermekte. Bir boğumun kendisiyle arasındaki mesafe 0, doğrudan bağlı olmadığı bir boğumlar arasındaki mesafe ise sonsuz sembolü ile işaret edilmekte. Örneğin n1 boğumundan n3 ve n4 boğumlarına doğrudan bir hat olmadığı için sonsuz sembolü kullanıldı. Algoritmanın becerisi sonsuz sembollerini eritmek ve hatta sayısal değer alan hücrelerde olabilecek daha kısa mesafeler var ise bunları matris üzerinde güncellemektir.

Örneğin n1'den n3'e direkt gidişimiz olmadığından sonsuz olarak işaretlenmiş durumda. Oysa ki n1->n2->n3 şeklinde bir ulaşım var. Yani n2 üzerinden geçiş yaparak n3'e varabiliriz. Elbette n3'e varmak için n6 üzerinden de hareket edebiliriz. Yani n1->n6->n3 şeklinde bir güzergah da söz konusu olabilir. Hatta n1->n5->n4->n3 şeklinde de gidebiliriz.

İşte matrisimizi bu şekilde algoritma içerisinde işleterek nihai haline getirmemiz gerekiyor. Tahmin edeceğiniz üzere bu, çok da uğraşmak isteyeceğimiz türden bir iş değil :) Bu yüzden zaten kod yolu ile ilgili algoritmayı çalıştırmayı tercih etmekteyiz. Aşağıda algoritmanın kullanımına ilişkin bir kod parçası yer almaktadır.

using System;
using System.Linq;

namespace FloydWarshallCode
{
    class Program
    {
        static void Main(string[] args)
        {
            double[][] proximityMatrix = PrepareFirstState();
            Solve(ref proximityMatrix);
            Dump(proximityMatrix);
        }

        public static void Solve(ref double[][] matrix)
        {
            int size = matrix.Count();

            for (int i = 0; i < size; i++)
            {
                for (int j = 0; j < size; j++)
                {
                    for (int k = 0; k < size; k++)
                    {
                        matrix[j][k] = Math.Min(matrix[j][k], matrix[j][i] + matrix[i][k]);
                    }
                }
            }
        }

        private static double[][] PrepareFirstState()
        {
            double[][] matrix = new double[6][]{
                new double[6],
                new double[6],
                new double[6],
                new double[6],
                new double[6],
                new double[6]
            };

            matrix[0][0] = 0;
            matrix[0][1] = 5;
            matrix[0][2] = double.PositiveInfinity;
            matrix[0][3] = double.PositiveInfinity;
            matrix[0][4] = 16;
            matrix[0][5] = 8;

            matrix[1][0] = 5;
            matrix[1][1] = 0;
            matrix[1][2] = 1;
            matrix[1][3] = double.PositiveInfinity;
            matrix[1][4] = double.PositiveInfinity;
            matrix[1][5] = 2;

            matrix[2][0] = double.PositiveInfinity;
            matrix[2][1] = 1;
            matrix[2][2] = 0;
            matrix[2][3] = 1;
            matrix[2][4] = double.PositiveInfinity;
            matrix[2][5] = 6;

            matrix[3][0] = double.PositiveInfinity;
            matrix[3][1] = double.PositiveInfinity;
            matrix[3][2] = 1;
            matrix[3][3] = 0;
            matrix[3][4] = 4;
            matrix[3][5] = 5;

            matrix[4][0] = 16;
            matrix[4][1] = double.PositiveInfinity;
            matrix[4][2] = double.PositiveInfinity;
            matrix[4][3] = 4;
            matrix[4][4] = 0;
            matrix[4][5] = 4;

            matrix[5][0] = 8;
            matrix[5][1] = 2;
            matrix[5][2] = 6;
            matrix[5][3] = 5;
            matrix[5][4] = 4;
            matrix[5][5] = 0;

            return matrix;
        }

        public static void Dump(double[][] matrix)
        {
            int size = matrix.Count();

            for (int i = 0; i < size; i++)
            {
                for (int j = 0; j < size; j++)
                {
                    Console.Write("{0}\t", matrix[i][j]);
                }
                Console.WriteLine();
            }
        }
    }
}

Console uygulamasının 3 önemli fonksiyonu vardır. İlk olarak makalemizin başında bahsettiğimiz yakınlık matrisinin birinci versiyonunu hazırlayan basit bir metod bulunur. Pek tabii gerçek hayat senaryolarında ilgili matrisin belli bir Graph kaynağından otomatik olarak hazırlanması söz konusudur. Uygulamayı çalıştırdığımızda aşağıdaki ekran görüntüsünde yer alan sonuç matrisini elde ederiz.

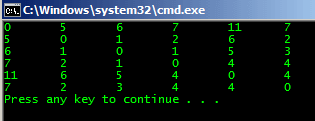
Buna göre bir noktadan bir noktaya gidilebilecek en kısa mesafeler bulunmuştur. Örneğin n3 noktasından n5 noktasına gitmek istediğimizde en kısa güzergah 5km uzunluğunda olup n3->n4->n5 rotası şeklindedir. Diğer alternatif yollara bakıldığında gerçekten de en kısa mesafenin bu olduğu açıkça görülebilir.

Görüldüğü üzere Floyd-Warshal, Graph tabanlı veri kümelerinde boğumlar arası en kısa mesafelerin buluması için kullanılabilecek basit ve hızlı algoritmalardan birisidir. Konu hakkında internet üzerinden de ulaşabileceğiniz bir çok kaynak mevcut. Bunları inceleyerek algoritmayı çalışma sistematiğini anlamaya çalışmanızı öneririm. Gerçek hayat vakalarına bakılmasında da yarar olduğu kanısındayım. Böylece geldik bir makalemizin daha sonuna. Tekrardan görüşünceye dek hepinize mutlu günler dilerim.