Merhaba Arkadaşlar,
Bir süredir yazılım dünyasında sıklıkla kullanılan basit algoritmalara merak salmış durumdayım. Bazıları kafayı yedirtecek cinsten olsalarda arada sırada bunları değerlendirmekte ve paslanan dimamızı açmaya çalışmakta yarar olduğu kanısındayım.
Aslına bakarsanız bilgisayar bilimlerinde uygulanabilen, gerçekten çok işe yarayan ve onları keşfedenleri saygıyla hatırlamamız gereken algoritmalar mevcut. Örneğin bunlardan birisi olan Levenshtein Distance algoritması ve mucidi Vladimir Levenshtein 
Bu algoritma bizlere, özellikle arama motorlarında da kullanılabilen bir model sunmaktadır. Son kullanıcıların aradıkları kelimeleri tam olarak belirleyemedikleri veya kestiremedikleri durumlarda, öneri olarak sunulan kelimelerin tespit edilmesi sırasında ele alınan bir algoritmadır. Örneğin ben Google sitesindeki arama kutucuğunda kendi ismimi eksik karakterler ile yazdığımda, google daha önceden yapmış olduğu indekslenmiş içeriklere göre bir öneri de bulunmuştur(Bunu mu demek istediniz kısmı) Aşağıdaki şekilde bu durum açık bir şekilde görülmektedir.
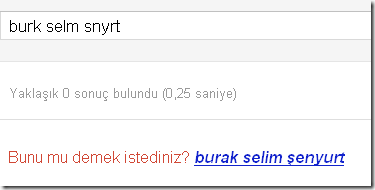
Arama motorları dışında, özellikle imla kontrolü yapan uygulamalarda da(Söz gelimi Microsoft Outlook veya Microsoft Word’ ün Spell Checking mekanizmalarında) bu algoritmanın kullanımına sıklıkla şahit olmaktayız.
Biz bu yazımızda söz konusu algoritmanın kullanılması için gerekli olan temel fonksiyonu, sıklıkla yaptığımız üzere bir Extension Method olarak geliştirmeye ve test etmeye çalışıyor olacağız. Ancak kodlama kısmına geçmeden önce algoritmanın nasıl çalıştığına ve işlediğine bakmamızda yarar olacağı kanısındayım.
Aslında algoritma temel olarak iki kelimenin birbirlerine olan benzerliklerini ölçümlemek amacıyla kullanılmaktadır. Sonuç tek bir sayısal değerdir ve iki kelimeden birinin diğerine dönüştürülebilmesi için gerekli olan işlem sayısını ya da maliyetini vermektedir. Çok doğal olarak bu sayınının düşük olması arzu edilen neticedir. Nitekim daha az değişiklik anlamına gelmektedir. Çok doğal olarak bir kelimenin, bir öneri kelime kümesi içerisindekiler ile karşılaştırılması sonucu ortaya çıkan sayısal değerlerden en küçüğü veya küçükleri, sonuca ulaşılması ve doğru önerilerde bulunulması açısından önemlidir.
Peki bu yakınlık değeri nasıl hesaplanmaktadır? 
Bunun için kelimeler arası iki boyutlu bir matris dizisi kullanılır. Lakin söz konusu matrisin içereceği değerlerin tespiti çok da kolay değildir. Dilerseniz aşağıdaki Excel görüntüsünde yer alan örneklemelere bir bakalım ve algoritmayı daha yakından tanımaya çalışalım.
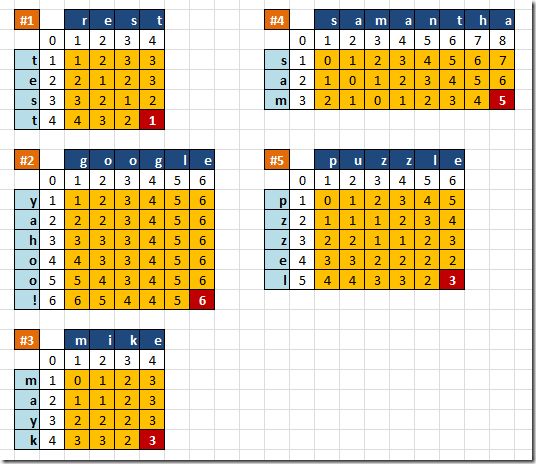
Bu grafikte, 5 farklı örnek ile 10 kelimenin birbirleri ile yakınlıklarının Levensthein Distance algoritmasına göre nasıl hesap edildiği gösterilmektedir. İlk olarak rest kelimesinin test kelimesi ile olan yakınlığı bulunmaya çalışılmıştır. Aslına bakarsanız bu iki kelime arasında sadece 1 işlem yaparak sonuca ulaşılabilir. Bu işleme göre rest kelimesindeki r harfi yerine, t harfinin gelmesi yeterlidir. Matris içerisinde yer alan sayılar o andaki sütuna veya satıra kadar olan harf topluluklarının birbirleri ile eş düşmeleri için gerekli işlem sayılarını içermektedir.
Şimdi de google ve yahoo! kelimelerinin yakınlık hesabını göz önüne alalım. Normal şartlarda iki kelime içerisinde ortak olan 2 “o” harfi bulunmaktadır ancak yerleri farklıdır. Diğer harfler ise zaten birbirlerinde yoktur. Bu nedenle 6 işlemlik bir operasyon yapılması gerekmektedir.
Peki sayılar tam olarak nasıl yerleştirilmekte veya okunmaktadırlar? Hemen Samantha ile Sam’ in karşılaştırılmasını ele alalım. Şimdi 0 indisli olacak şekilde 1nci sütun ve 1inci satırı göz önüne alalım. 1nci sütunda “s” harfi ve 1nci satırda yine “s” harfi bulunmaktadır. Dolayısıyla o anki karşılaştırmada, her iki harfte aynı olduğunda bir işlem yapılmasına gerek yoktur. Dolayısıyla işlem maliyeti 0dır. Şimdi 2ncü sütuna ve 1nci satıra bakalım. 2nci sütuna kadar olan kısımda “sa“ hecesi oluşmuştur. Satır tarafında ise sadece “s” harfi bulunmaktadır. Dolayısıyla eşleştirme için satır kısmındaki “s” harfine bir de “a” harfinin eklenmiş olması gerekir. Ki bu da 1 işlem maliyeti olarak ifade edilmektedir.
Durumu biraz daha öteleyelim. 5 numaralı örnekte yer alan puzzle ve pzzel kelimelerinin karşılaştırılmasında 5nci sütun ve 4ncü satıra bakalım. 5nci sütuna kadar puzz kelimesi 4ncü satıra kadar da pzz kelimesi söz konusudur.pzz’ un puzz kelimesine benzemesi için araya bir “u” harfinin konulması yeterlidir. Diğer kısımlar satır ve sütun bazında da eşleşmektedir. Bu yüzden buradaki işlem maliyeti değeri 1 dir. Ancak yine 0 indisli baktığımızda ve 7nci sütun ve 6ncı satıra kadar olan kısımda puzzle ve pzzel kelimeleri göz önüne alındığında ise; pzzel’ dan puzzle’a geçmek istenildiğinde ilk olarak araya bir “u” harfi konulur.
puzzel
Ardından “el” hecesinde e’ nin l yerine, l’ nin e yerine geçmesi gerekir.
puzzle
Dolayısıyla toplamda 3 işlem maliyeti söz konusu olmuştur.
Bu algoritma gereği iki kelime arasındaki yakınlık derecesi, matrisin sağ alt hücresindeki sayısal değer ile ifade edilmektedir. Buna göre puzzle ile pzzel kelimeleri arasındaki mesafe 3 işlem operayonu ile ölçülürken, bu Samantha ve Sam kelimeleri arasında 5 işlemlik bir maliyet oluşması söz konusudur(Samantha’ dan antha kısmının atılması nedeni ile 5 işlemlik bir maliyet oluşmaktadır)
Algoritmayı biraz kavradığımıza göre dilerseniz bunu C# tarafında bir Extension Method içerisine dahil edelim ve test uygulamamıza çıkalım. Bu amaçla aşağıdaki örnek Console uygulamasını göz önüne alabiliriz.
using System;
namespace UsingLevenshtein
{
class Program
{
static void Main(string[] args)
{
TestMethod("rest", "test");
TestMethod("google", "yahoo!");
TestMethod("mike", "mayk");
TestMethod("samantha", "sam");
TestMethod("puzzle", "pzzel");
}
private static void TestMethod(string Source,string Target)
{
int[,] matrix3 = new int[Source.Length, Target.Length];
int distance3 = Source.FindLevenshteinDistance(Target, out matrix3);
Console.WriteLine("{0} vs {1}\nDistance : {2}\n",Source,Target, distance3);
WriteToConsole(matrix3);
}
static void WriteToConsole(int[,] Matrix)
{
for (int i = 0; i < Matrix.GetLength(0); i++)
{
for (int j = 0; j < Matrix.GetLength(1); j++)
{
Console.Write("\t{0} ", Matrix[i, j]);
}
Console.WriteLine();
}
Console.WriteLine();
}
}
public static class StringExtensions
{
// Genişletme metodu, karşılaştırma matrisini de out parametresi olarak döndürmektedir.
public static int FindLevenshteinDistance(this string Source, string Target,out int[,] Matrix)
{
int n = Source.Length;
int m = Target.Length;
Matrix = new int[n + 1, m + 1]; // Hesaplama matrisi üretilir. 2 boyutlu matrisin boyut uzunlukları ise kaynak ve hedef metinlerin karakter uzunluklarına göre set edilir
if (n == 0) // Eğer kaynak metin yoksa zaten hedef metnin tüm harflerinin değişimi söz konusu olduğundan, hedef metnin uzunluğu kadar bir yakınlık değeri mümkün olabilir
return m;
if (m == 0) // Yukarıdaki durum hedefin karakter içermemesi halinde de geçerlidir
return n;
// Aşağıdaki iki döngü ile yatay ve düşey eksenlerdeki standart 0,1,2,3,4...n elemanları doldurulur
for (int i = 0; i <= n;i++)
Matrix[i, 0] = i;
for (int j = 0; j <= m; j++)
Matrix[0, j] = j;
// Kıyaslama ve derecelendirme operasyonu yapılır
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
int cost = (Target[j - 1] == Source[i - 1]) ? 0 : 1;
Matrix[i, j] = Math.Min(Math.Min(Matrix[i - 1, j] + 1, Matrix[i, j - 1] + 1), Matrix[i - 1, j - 1] + cost);
}
return Matrix[n, m]; // sağ alt taraftaki hücre değeri döndürülür
}
}
}
Uygulamamız içerisinde dikkat edeceğiniz üzere Excel tablosunda yer alan kelimelere ait bir test işlemi gerçekleştirilmektedir.FindLevenshteinDistance isimli metodumuz bir genişletme fonksiyonu olarak herhangibir string tipine uygulanabilecek şekilde tasarlanmıştır. Bununla birlikte söz konusu metod hem Levenshtein Distance matrisini, hemde yakınlık derecesini döndürmektedir. Uygulama içerisinde kelimeler arası testi kolaylaştırmak adına TestMethod isimli bir fonksiyon da ele alınmıştır. Programın çalışma zamanındaki çıktısı ise aşağıdaki gibi olacaktır.
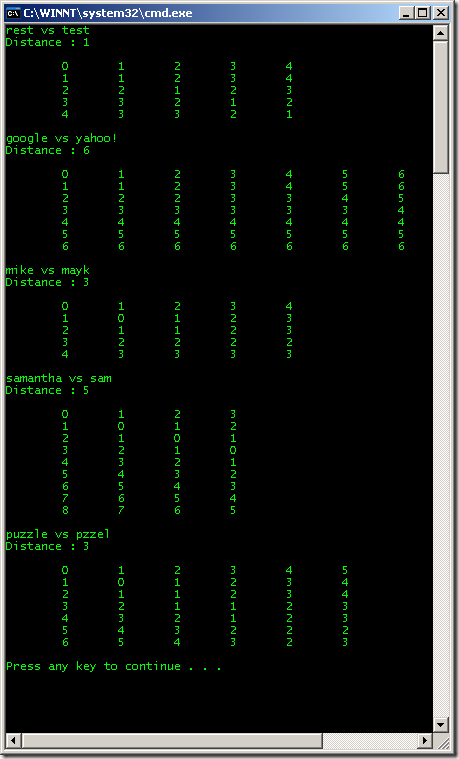
Artık bundan sonrasında yapılması gereken, bir text kutucuğuna girilen metni, bir metin kümesi içerisinde söz konusu algoritmaya göre aramak ve yakınlık derecesi, bir başka deyişle operasyon işlem maliyeti en düşük olan kelime veya kelimeleri kullanıcıya sunmaya çalışmaktan ibarettir. Dilerseniz bu konuyu bir düşünün ve uygulamaya çalışın Tekrardan görüşünceye dek hepinize mutlu günler dilerim.
UsingLevenshtein.zip (15,85 kb)