Merhaba Arkadaşlar,
İnsan hafızası gizemli çalışan ama çoğu zamanda bizleri şaşırtan bir mekaniğe sahiptir. Doğduğumuz andan itibaren 3 yaşına kadar geçen zaman dilimi içerisinde görsel olarak ne izlersek kaparız. Ancak neredeyse bunların hiç birini hatırlamayız.
Çocukluğumuz, ergenliğimiz, yetişkinliğimiz, orta yaş halimiz ve yaşlılığımız. Tüm bu zaman dilimlerinde beynimiz sürekli olarak bir şeyleri hafıza da tutma ihtiyacı hisseder. Zaman zaman öğrendiğimiz pek çok bilgiyi kolayca unutur ve ihtiyacımız olduğunda hatırlamakta zorlanırız. Ama kimi bilgilerde bilinç altımıza neredeyse kazınır ve geçerli bir sağlık problemi oluşmadığı sürece hiç unutmayız(Çarpım tablosu, matematik dört işlemin nasıl yapıldığı veya hangi ışıkta durulması gerektiği gibi)
Peki kolayca unutabileceğimiz bilgiler nasıl oluşurlar? 
Genelde öğrendiklerimizi çok sık kullanmadığımız veya tekrar etmediğimiz durumlarda unutmak kaçınılmaz gerçeklerden birisidir. Kullanmama süresi arttığında ise, ihtiyaç duyulduğu anda söz konusu bilgileri tekrardan hatırlamak da giderek zorlaşmaktadır. Aslında çok sık kullanılmayan ama yaşamın herhangibir anında ihtiyaç duyabileceğimiz bilgileri yazarak bir yerlerde saklamak, mücadele etme yollarından birisidir.
Örneğin Üniversitede okutulan veri yapıları ve algoritmalar derslerini düşünelim. Öğrenmek, kavrayabilmek, kodlarını geliştirebilmek için epey kafa patlattığımız zorlayıcı bu içerikler, kolayca unutulabilecek cinstendir 
Tabi eğer bunları her dönem anlatan bir akademisyen veya sürekli matematik modeller geliştiren bir uzman değilseniz. Eğer ki, .Net Framework, Java EE, SAP gibi ortamları kullanarak ağırlıklı olarak veri odaklı uygulamalar geliştiriyorsanız, zaten bu ders içeriğinin yakınından çok nadir olarak geçersiniz. İşte ben de bu hafıza kaybını yaşadığım şu dönemlerde, eski bilgilerimi hatırlamaya çalışmak istedim. İlk gözüme kestirdiğim konu ise ikili ağaç yapısı(Binary Tree) ve bunun üzerinden arama, ekleme gibi temel işlemlerin nasıl yapıldığı oldu?
İkili ağaç yapısı basitliği ve hızlı sonuç üretimi açısından bakıldığında, arama algoritmalarından tutunda oyun programlamaya, ilişkisel veri tabanlarından, karmaşık matematik modellere kadar pek çok alanda kullanılmaktadır. Binary Tree veri yapısı ve bu yapı üzerinde gerçekleştirilecek çeşitli operasyonlar(arama, ekleme, silme gibi) göz önüne alındığında ilk etapta bu ağacın nasıl oluşturulduğunun kavranması gerekmektedir. Aslında ikili ağaçlar, şirketlerin organizasyon ağacına benzer bir içeriğe sahiptirler. Tabi teknik olarak düşündüğümüzde bu ağacı oluşturmanın bazı kuralları vardır. Şimdi gelin teknik terim karmaşası içerisine girmeden konuyu bir örnek üzerinde kavramaya çalışalım.
Elimizde şöyle bir sayı dizisi olduğunu düşünelim.
7,4,9,1,3,10,12,8,5,6,9,11
Şimdi bu rakamsal dizinin Binary Tree grafiğini oluşturmaya çalışalım.
İlk olarak 7 rakamından başlayıp, bunun Kök Boğum(Root Node) olduğunu düşünerekten en başa yerleştirelim. Ardınan ikinci rakama geçelim. İkinci rakam, ilk rakam olan 7' ye bağlı olmak durumda. Bir başka deyişle onun alt boğumu/çocuk boğumu(Child Node) olacak. 4, 7' den küçük bir rakam. Bu sebepten onu sol alt tarafa alalım.
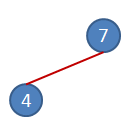
3ncü rakamımız ise 9. Root Node ile karşılaştırdığımızda ondan büyük olduğunu görüyoruz. Bu yüzden onu 7nin sağ alt node' u olacak şekilde grafiğimize yerleştirelim.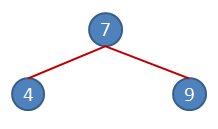
Hımmm...
Demek ki bir kuralımız var. "Bir node değeri eğer bağlı olduğu node' un içindeki değerden küçükse onun solunda, değilse sağında yer alıyor olmalı."
4ncü rakamdan devam edelim.1, root node olan 7den küçük. Dolayısıyla sol dalda yer almalı. Ancak sol dalda 4 değeri de var. 1, 4ten küçük olduğundan ve az önce bahsettiğimiz kuraldan dolayı sol alt node olarak grafiğe eklenmeli.
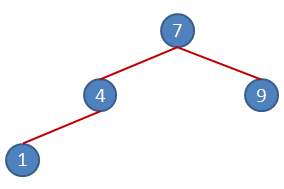
5nci rakamımız ise 3. Yine Root Node' dan aşağıya doğru inmeye başlıyoruz. Kuralımıza göre 3, 7den küçük ve onun sol dalında yer almalı. Bir alt seviyeye indiğimizde 4 ile karşılaşılıyor. 3, 4ten küçük olduğu için kuralımıza göre sol alt node olmalı ama yol devam ediyor. Çünkü sol alt node' da 1 var. 3, 1den büyük olduğu için kuralımıza göre sağ alt node' olmalı.
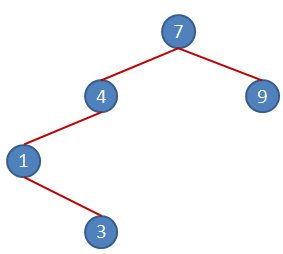
6ncı rakamımız 10. 10, root node olan 7den büyük olduğu için kuralımıza göre sağ dalda yer almalı. Sağ daldan aşağıya doğru indiğimizde 1nci seviyede 9 olduğunu görüyoruz. 10, 9dan büyük olduğu için sağ alt node' unda yer almalı.
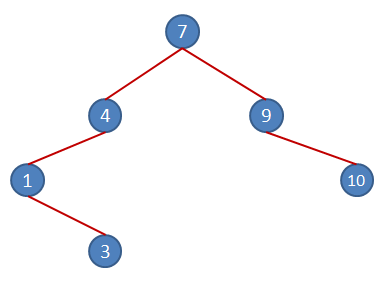
7nci rakamımız 12. Yine Root Node ile kıyaslayarak başladığımızda kuralımıza göre sağ dalda olması gerekiyor. 12, 9 dan büyük olduğu için sağ daldan inmeye devam ediyor ve yine 10dan büyük olduğu için sağ alt node olarak 3ncü seviyedeki yerini alıyor.
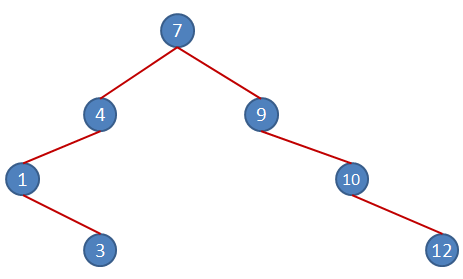
8nci elemanımız ise 8. Root node olan 7den büyük olduğu için sağ daldan aşağıya doğru akması gerekiyor. Yol üstünde ilk olarak karşılaştığı 9dan küçük olduğu içinse sol alt node olarak 2nci seviyedeki yerini alıyor.
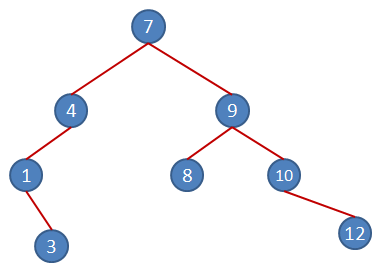
9ncu elemanımız 5. Root Node olan 7den küçük olduğu için kuralımıza göre sol daldan aşağıya doğru kaydırılması gerekiyor. 1nci seviyede karşılaştığımız 4ten büyük bir değer olduğu içinse sağ alt node olarak 2nci seviyedeki yerini alıyor.
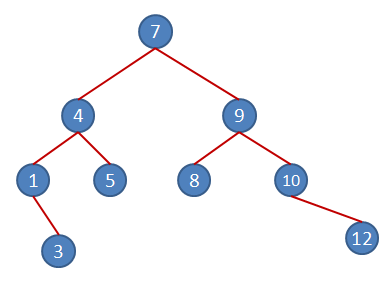
10ncu elemanımız 9. Ancak 9 zaten rakam dizimizde bir kez kullanıldı ve bir kere daha kullanılmaması gerekiyor. Hımm...Öyleyse bir kural daha ortaya çıkıyor.
"Zaten dizide var olan bir elemanı ağaça tekrardan ekleyemeyiz."
Örneğimizde yer alan son elemanımız ise 11. Yine root node ile başladığımızda 7den büyük olduğu için kuralımıza göre sağ dalda yer alması gerekiyor. Rakamı sağ daldan aşağıya doğru kaydırdığımızda, 1nci seviyedeki 9dan büyük olduğunu görüyoruz. Buna göre sağ daldan devam edilmeli. Sıradaki 10 rakamından da büyük olduğundan yine sağ dalda kalmalı. Sonradan gelen 12 rakamından küçük olduğu içinse sol alt dal olarak son seviyede yerini almalı.
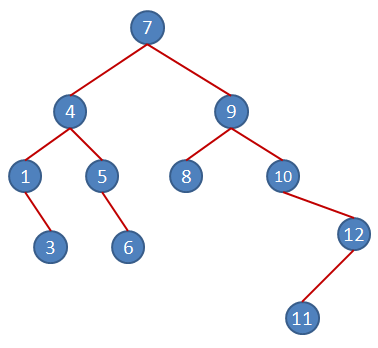
Daha başka sayımız kalmadığı için Binary Tree grafiğini tamamlamış bulunuyoruz. Görüldüğü gibi Root Node' dan aşağıda doğru inen ağaç yapısında her boğuma en fazla iki boğum bağlanabilmektedir(Zaten Binary denmesinin sebebi de budur 
). Bunun temel sebebi ise büyük ve küçük olma durumuna göre ilgili boğumun sağ veya sol alt boğum olarak grafiğe ekleniyor olmasıdır. Tabi bunun dışında zaten ağaç içerisinde yer almış bir elemanın tekrardan yer almaması gerekliliği ortaya konulmuştur. Dallar haricinde aslında boğumlar belirli seviyelere denk gelirler. Tüm bu bilgiler ışığında sayı dizisinin Binary Tree grafiği aşağıdaki nihai halini alır.
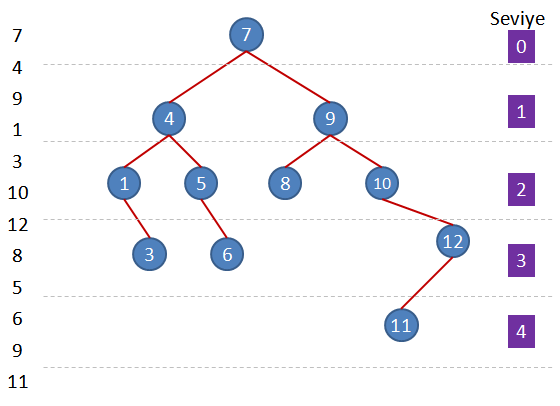
Peki bu tip bir ağaç yapısını programatik ortamda tasarlamak istersek?
Aslında bu ağaç yapısı içerisinde dolaşmak bile başlı başına bir iş. Kağıt üzerinde her ne kadar kolay olsa da teorik olarak bunun bilinen 3 yöntemi bulunmaktadır. Traverse adı verilen bu dolaşım teknikleri InOrder(Sol dalı dolaş, root' a uğra, sağ dalı dolaş), PreOrder(Root' dan başla, sol dalı yukarıdan aşağı gez, sol dalı yukarıdan aşağı gez) ve PostOrder(Sol dalı aşağıdan yukarı tara, sağ dalı aşağıdan yukarı tara, root' a uğra) olarak geçmektedir.
Ne yazık ki .Net Framework tarafında Binary Tree yapısını destekleyen hazır bir tip ve özellikle koleksiyon bulunmamaktadır. Dolayısıyla bunu kendimiz oluşturmak durumundayız. Biraz uğraştırıcı olsa da buna hizmet edecek bir geliştirme yapabiliriz. Bize iki temel tip gerekmektedir. Birincisi ağaç yapısındaki her bir boğumu temsil edecek olan tiptir. Bu tip bir Node' un değerini, kendinden sonraki Sol ve Sağ Node' ları ve bağlı olduğu Parent Node' u bilecek şekilde tasarlanmalıdır. Yani aşağıdaki gibi.
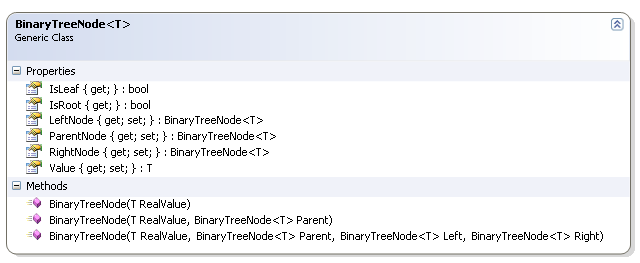
public class BinaryTreeNode<T>
{
public T Value { get; set; }
public BinaryTreeNode<T> ParentNode { get; set; }
public BinaryTreeNode<T> LeftNode { get; set; }
public BinaryTreeNode<T> RightNode { get; set; }
public bool IsRoot { get { return ParentNode == null; } }
public bool IsLeaf { get { return LeftNode == null && RightNode == null; } }
public BinaryTreeNode(T RealValue)
{
Value = RealValue;
}
public BinaryTreeNode(T RealValue, BinaryTreeNode<T> Parent)
{
Value = RealValue;
ParentNode = Parent;
}
public BinaryTreeNode(T RealValue, BinaryTreeNode<T> Parent, BinaryTreeNode<T> Left, BinaryTreeNode<T> Right)
{
Value = RealValue;
RightNode = Right;
LeftNode = Left;
ParentNode = Parent;
}
}
Bu basit bir tip. Asıl önemli olan ağacın grafiğini kodsal olarak sembolize edecek, Add, Remove ve Traverse gibi işlemlerini yapacak olan tipi geliştirmek. Onu da biraz uğraştıktan sonra aşağıdaki gibi yazabiliriz.
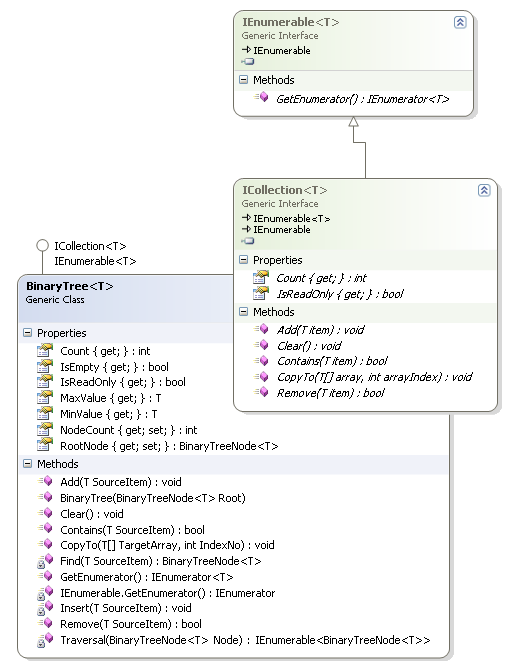
Dikkat edileceği üzere BinaryTree sınıfı generic olarak tasarlanmış ve ICollection<T> ile IEnumerable<T> arayüzlerini(Interface) uygulamıştır. Bu nedenle zorunlu olarak ezmesi gereken bazı üyeleri vardır. Ayrıca BinaryTree içerisinde yer alacak olan BinaryTreeNode nesne örneklerinin en azından değer bazında karşılaştırma yapılabilir olması gerekmektedir. Nitekim değerlerin bibirlerinden büyük ve küçük olma durumlarına göre bir yerleştirme ve arama söz konusudur. Bu yüzden bir de generic Constraint konularak T tipinin IComparable<T> arayüzünü uygulama zorunluluğu konulmuştur. Sınıfımıza ait kodlar ise aşağıdaki gibidir.
public class BinaryTree<T>
: ICollection<T>, IEnumerable<T>
where T : IComparable<T>
{
public BinaryTreeNode<T> RootNode { get; set; }
public int NodeCount { get; set; }
public bool IsEmpty { get { return RootNode == null; } }
// Ağaç içerisindeki en küçük değerli elemanı döndürür
public T MinValue
{
get
{
if (IsEmpty)
throw new Exception("Ağaç içerisinde hiç bir eleman yok");
BinaryTreeNode<T> tempNode = RootNode;
while (tempNode.LeftNode != null) // Sol dallarda değer olduğu sürece dolaş
tempNode = tempNode.LeftNode;
return tempNode.Value;
}
}
// Ağaç içerisindeki en büyük değerli elemanı döndürür
public T MaxValue
{
get
{
if (IsEmpty)
throw new Exception("Ağaç içerisinde hiç bir eleman yok");
BinaryTreeNode<T> tempNode = RootNode;
while (tempNode.RightNode != null) // Sağ dallarda değer olduğu sürece dolaş
tempNode = tempNode.RightNode;
return tempNode.Value;
}
}
// Kaç eleman olduğunu döndürür
public int Count
{
get { return NodeCount+1; }
}
public BinaryTree(BinaryTreeNode<T> Root)
{
RootNode = Root;
NodeCount = 0;
}
public IEnumerator<T> GetEnumerator()
{
foreach (BinaryTreeNode<T> tempNode in Traversal(RootNode))
yield return tempNode.Value; // Çok şükürki 2.0 ile gelen yield keyword' ü var :)
}
IEnumerator IEnumerable.GetEnumerator()
{
foreach (BinaryTreeNode<T> tempNode in Traversal(RootNode))
yield return tempNode.Value;
}
// Koleksiyona eleman ekleyebilmek için kullanılır
public void Add(T SourceItem)
{
if (RootNode == null)
{
RootNode = new BinaryTreeNode<T>(SourceItem);
NodeCount++;
}
else if(Contains(SourceItem))
return;
else
Insert(SourceItem);
}
public void Clear()
{
RootNode = null;
}
// Koleksiyonda T tipinden olan eleman olup olmadığını araştırır
public bool Contains(T SourceItem)
{
if (IsEmpty)
return false;
BinaryTreeNode<T> tempNode = RootNode;
while (tempNode != null)
{
int comparedValue = tempNode.Value.CompareTo(SourceItem);
if (comparedValue == 0)
return true;
else if (comparedValue < 0)
tempNode = tempNode.LeftNode;
else
tempNode = tempNode.RightNode;
}
return false;
}
// Koleksiyon içeriğinin aynı tipten bir Array' e kopyalar
public void CopyTo(T[] TargetArray, int IndexNo)
{
T[] tempArray = new T[NodeCount+1];
int Counter = 0;
foreach (T value in this)
{
tempArray[Counter] = value;
Counter++;
}
Array.Copy(tempArray, 0, TargetArray, IndexNo, this.NodeCount);
}
// Koleksiyondan eleman çıkartmak için kullanılır
public bool Remove(T SourceItem)
{
BinaryTreeNode<T> item = Find(SourceItem);
if (item == null)
return false;
List<T> values = new List<T>();
foreach (BinaryTreeNode<T> tempNode in Traversal(item.LeftNode))
values.Add(tempNode.Value);
foreach (BinaryTreeNode<T> tempNode in Traversal(item.RightNode))
values.Add(tempNode.Value);
if (item.ParentNode.LeftNode == item)
item.ParentNode.LeftNode = null;
else
item.ParentNode.RightNode = null;
item.ParentNode = null;
foreach (T value in values)
Add(value);
return true;
}
public bool IsReadOnly
{
get { return false; }
}
BinaryTreeNode<T> Find(T SourceItem)
{
foreach (BinaryTreeNode<T> item in Traversal(RootNode))
if (item.Value.Equals(SourceItem))
return item;
return null;
}
// InOrder modeline göre elemanlar dolaşılır.
IEnumerable<BinaryTreeNode<T>> Traversal(BinaryTreeNode<T> Node)
{
if (Node.LeftNode != null)
foreach (BinaryTreeNode<T> leftNode in Traversal(Node.LeftNode))
yield return leftNode;
yield return Node;
if (Node.RightNode != null)
foreach (BinaryTreeNode<T> rightNode in Traversal(Node.RightNode))
yield return rightNode;
}
void Insert(T SourceItem)
{
BinaryTreeNode<T> tempNode = RootNode;
bool found = false;
while (!found)
{
int comparedValue = tempNode.Value.CompareTo(SourceItem);
if (comparedValue < 0)
{
if (tempNode.LeftNode == null)
{
tempNode.LeftNode = new BinaryTreeNode<T>(SourceItem, tempNode);
NodeCount++;
return;
}
else
{
tempNode = tempNode.LeftNode;
}
}
else if (comparedValue > 0)
{
if (tempNode.RightNode == null)
{
tempNode.RightNode = new BinaryTreeNode<T>(SourceItem, tempNode);
NodeCount++;
return;
}
else
{
tempNode = tempNode.RightNode;
}
}
else
{
return;
}
}
}
}
Artık yeni tiplerimizi denemeye çıkabiliriz. Bu amaçla program kodunda aşağıdaki test kodları göz önüne alınabilir.
class Program
{
static void Main(string[] args)
{
BinaryTree<int> numbers = new BinaryTree<int>(new BinaryTreeNode<int>(7));
numbers.Add(4);
numbers.Add(9);
numbers.Add(1);
numbers.Add(3);
numbers.Add(10);
numbers.Add(12);
numbers.Add(8);
numbers.Add(5);
numbers.Add(6);
numbers.Add(9);
numbers.Add(11);
Console.WriteLine("{0} eleman aktarıldı", numbers.Count);
foreach (int number in numbers)
Console.WriteLine(number);
Console.WriteLine("{0} değeri koleksiyonda {1}",5,numbers.Contains(5)?"Var":"Yok");
Console.WriteLine("Max {0} Min {1}",numbers.MaxValue,numbers.MinValue);
int[] array = new int[numbers.Count];
numbers.CopyTo(array, 0);
}
}
Temel olarak koleksiyonumuza eklediğimiz temel operasyonlardan bazılarını kullanmaya çalıştık. Uygulamanın Runtime çıktısı aşağıdakine benzer olacaktır.
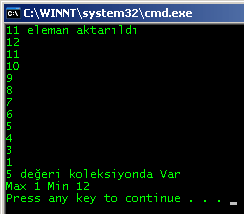
Tabi kodda gözden kaçırdığım bazı noktalar olabilir. Ben elimden geldiğince test etsem de farklı gözlerin bakmasında yarar var. Ancak temel olarak Binary Tree veri yapısını, C# ile nasıl kodlanabileceğini kavradığınızı düşünüyorum. Böylece geldik bir yazımızın daha sonuna. Tekrardan görüşünceye dek hepinize mutlu günler dilerim
BinarySearchTree.zip (42,36 kb)