 Merhaba Arkadaşlar,
Merhaba Arkadaşlar,
Matematik tek evresenl dil olarak varoluşumuzdan bu yana yaşamın içerisinde. Onun diğer bilimlere olan pozitif etkisi tartışılamaz. Bugün ulaştığımız noktada teknoloji sınırlarını zorlarken yüz yıllar öncesinden ispat edilmiş pek çok teoremin uygulanabilirliklerine de rastlıyoruz. Doğruyu söylemek gerekrise 1999 yılında ilk işe başladığımdan beri matematik'ten epey uzakta sadece kod yazmaktayım. Belki de bugün .Net Core'un Linux üzerinde koşturulup bir Cloud platformuna taşınması da önemli bir mevzu. Lakin o hayranlık duyduğumuz fikirlerin arkasında, çok fazla ilişmediğimiz(belki de bakmaya korktuğumuz) güçlü bir matematik var. Bende büyük bir cesaretle o fikirlerden birisinin arkasında olan matematiği bir nebze olsun anlamak istedim. Matematik kesin kuralları olan bir dil olduğu içi, yazdığım şeyleri doğru telafüz etmem gerekiyor. Eğer basit bir şekilde anlatabilirsem, konuyu da anlamış sayılırm(Son gün notu: Basitleştiremedi)
Geçtiğimiz iki hafta boyunca neredeyse her gün yarım saatimi ayırdığım ve anlamak için çaba sarf ettiğim bir konu oldu. Blockchain'in kullandığı Elliptic Curve Cryptography(ECC) algoritmasının nasıl çalıştığını öğrenmek. Araştırmalarıma başladığımda olayın içerisinde matematiğin bilgisayar şifreleme teknikleri üzerine kullanılan bir çok teorisine denk geldim. 1993 yılında girdiğim Matematik Mühendisliği bölümünde okurken gördüğüm pek çok konu burada da yer alıyordu. Ama zaman içerisinde hepsini unutmuşum. İkinci ve üçüncü dereceden denklemler, eliptik eğriler, asal sayılar, gruplar, sonlu alanlar(Finite Fields), Fermat'nın küçük teoremi(Little Theorem), modüler aritmetik, ayrık logaritma problemi(discrete logarithm problem), double and add algoritması, euclid vs... Aslında her şey Blockchain sisteminde yer alan eliptik eğri denklemine ait grafik gösterimin, gerçek sayılar ile ifade edileninden çok daha farklı olduğunu öğrenmemle başladı diyebilirim.
Örneğin Bitcoin, secp256k1 isimli ve aşağıdaki eşitlikle ifade edilen eliptik eğri denklemini kullanmakta. secp256k1' deki sec, Standards for Efficent Cryptography anlamına gelirken 256 değeri asal sayının kaç bit olduğunu ifade etmektedir. Sonlara doğru bu kavramları anlayacağım/anlatabileceğim diye umut ediyorum.
y2=x3+7
Gerçek sayılar için olan gösterimi şöyle;
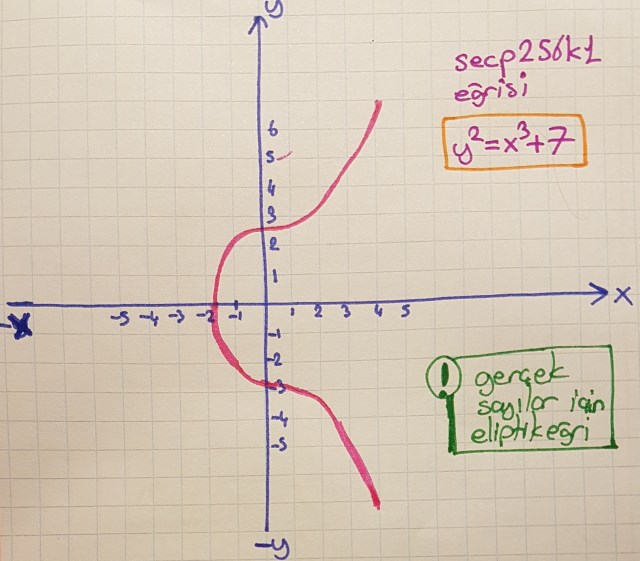
Toplam eleman sayısı asal olacak şekilde oluşturulmuş bir sonlu alan dizilimi için olan gösterimi ise şu şekilde;

Merak uyandırdı değil mi? Öyleyse ilk konumuz ile başlayalım.
Eliptik Eğriler
Eliptik eğri denklemlerine geçmeden önce bir kaç basit denklemi de hatırlamamız lazım. Doğrusal, ikinci dereceden ve üçüncü dereceden denklemleri ve x,y düzlemindeki gösterimlerini görünce sizler de hatırlayacaksınız?
y=ax+b , doğru denklemi
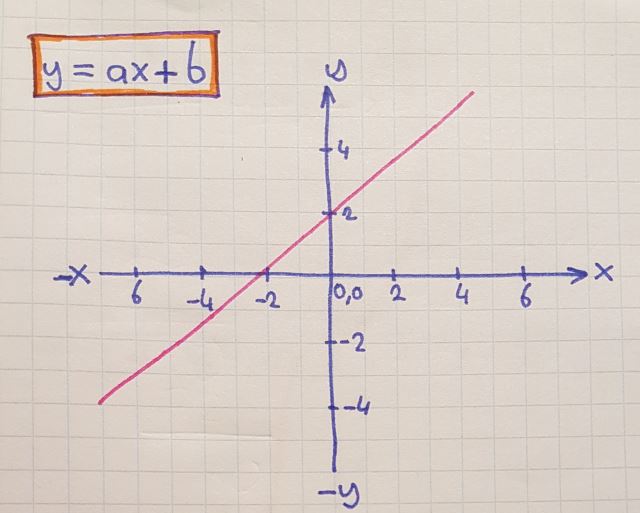
y=ax2+bx+c , parabol denklemi
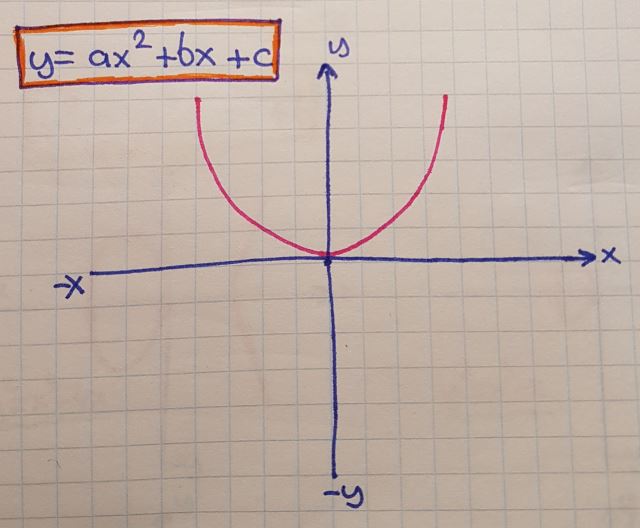
y=ax3+bx2+cx+d , 3ncü dereceden denklem
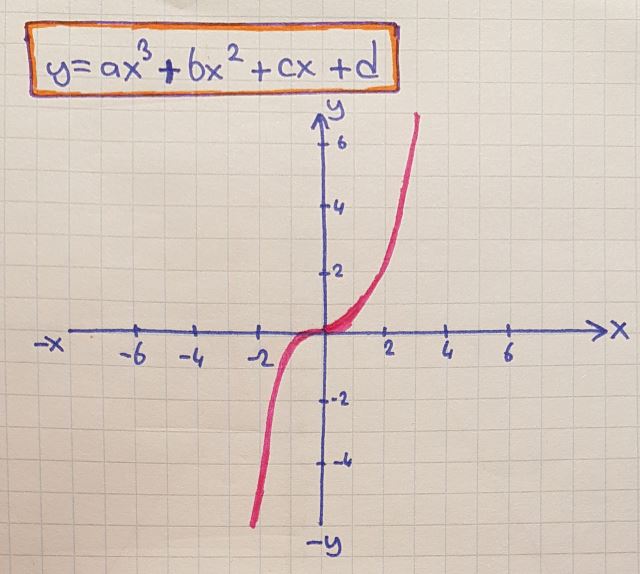
ve tabii konumuz olan eliptik eğri denklemi.
y2=x3+ax+b
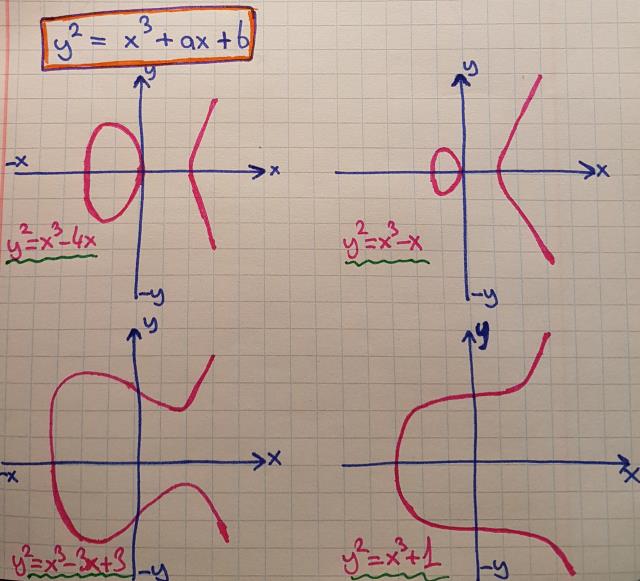
Yukarıdaki şekilde denkleme ait bir kaç farklı örnek görmektesiniz. Her ne kadar ben çok iyi çizemesemde, özellikle x ekseni özelinde simetriklik olduğunu söyleyebiliriz. Bazı hallerde iki ayrı eğri ve bazı hallerde de bu iki eğrinin birleştiği grafikler söz konusu. y2 den kaynaklı bir durum olduğu aşikar. Eliptik eğrilerin enteresan bir özelliği de vardır. Eğri üzerinde olduğu bilinen iki koordinat söz konusu olduğunda, bu koordinatların x değerleri birbirinden farklı olmak şartıyla, her iki koordinatın toplamından yine eğri üzerine denk düşen 3ncü bir koordinatı bulmamız mümkündür. Bulunuş şekli matematik severler için hayranlık uyandırıcıdır. Aşağıdaki şekille konuyu anlatmaya çalışayım.
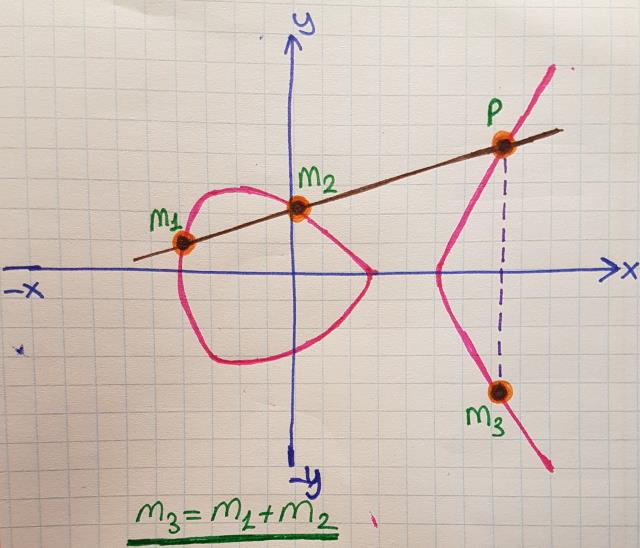
Şekilde M3 noktasını bulunuşu ifade edilmektedir. Olay şöyle başlar. Eğri üzerinden bilinen iki nokta referans alınır. x değerleri birbirlerinden farklı olan iki nokta. Bu noktaların üstünden geçen bir doğru çizilir. Çizilen doğru eğriyi 3ncü bir noktada daha kesecektir(örneğimizdeki P noktası) Bu noktanın iz düşümü de simetrik taraftaki bir noktaya denk gelmektedir(örneğimizdeki M3) İşte teoriye göre M1 ve M2 noktalarının toplamı M3 noktasını elde etmemizi sağlamaktadır. Tabii toplam dediğimiz olay biraz daha farklı. Noktayı bulmak için aşağıdaki gibi sıralanmış bir formül takımından yararlanılır.
3ncü noktanın bulunmasında ilk iki noktanın sıralı olması şart değildir. Sadece eğri üzerinde olduğu bilinen iki noktanın üzerinden geçen doğrunun kestiği üçüncü noktanın x düzlemindeki iz düşümü önemlidir.
Eğri denklemimiz : y2 = x3 + ax + b
M1 = (x1,y1) , M2 = (x2,y2), M1 + M2 = (x3,y3)
x1 ve x2 eşit olmadığı sürece
Eğim s = (y2 - y1) / (x2 - x1)
x3 = s2 - x2 - x1
y3 = s(x1 - x3) - y1
Kafamızı çok fazla bulandırmadan 3ncü nokta bulmanın nasıl yapıldığını basit bir örnekle inceleyelim.
y2=x3+5x+7
P1 = (2,5) , P2 = (3,7) => P3 = ?
52= 25 = 23+(5*2)+7 (P1 noktası eğri üzerinde)
72= 49 = 33+(5*3)+7 (P2 noktası eğri üzerinde)
s = (7 - 5) / (3 - 2) = 2 (Eğimi bulduk)
x3 = 22 - 2 - 3 = -1
y3 = 2(2 - (-1) ) - 5 = -1
P3 = (-1,1)
12= 1 = -13+(5*(-1))+7 (P3 noktası eğri üzerinde)
Şimdi örnekte neler oldu anlamaya çalışalım. Denklem ortada. İki tane noktamız var. Öncelikle bu noktaların eğri üzerinde olup olmadıklarının sağlamasını yapıyoruz. Sonrasında eğim değerini(s) bulmamız gerekiyor. Eğim bulunduktan sonra bu değerden yararlanarak x3 bilinmeyenini ve x3'ü de işin içerisine katarak y3 değerini hesaplıyor ve 3ncü noktanın koordinatlarını bulmuş oluyoruz. Son aşamada yine x3,y3 noktasının eliptik eğri üzerinde olup olmadığının sağlamasını gerçekleştiriyoruz. Bunu program kodu ile de deneyimleyebiliriz. Özellikle Python gibi diller bu tip matematiksel işlemler için kolaylıklar sunmakta.
p1=(2,5)
p2=(3,7)
def isOnCurve(p):
"""
p1 egri ustunde mi bakalim
"""
(x,y)=p1
return y**2 == x**3+(5*x)+7
def findSlope(p1,p2):
"""
p1 ve p2den yararlanarak egimi buluyoruz
"""
(x1,y1)=p1
(x2,y2)=p2
s=(y2-y1)/(x2-x1)
return s
def findThirdPoint(p1,p2,s):
"""
p1 ve p2den yararlanip 3ncu noktanin bulunmasi
"""
(x1,y1)=p1
(x2,y2)=p2
x3=s**2-x2-x1
y3=s*(x1-x3)-y1
return (x3,y3)
print p1,"is on curve?",isOnCurve(p1)
print p2,"is on curve?",isOnCurve(p2)
print findSlope(p1,p2)
print findThirdPoint(p1,p2,findSlope(p1,p2))
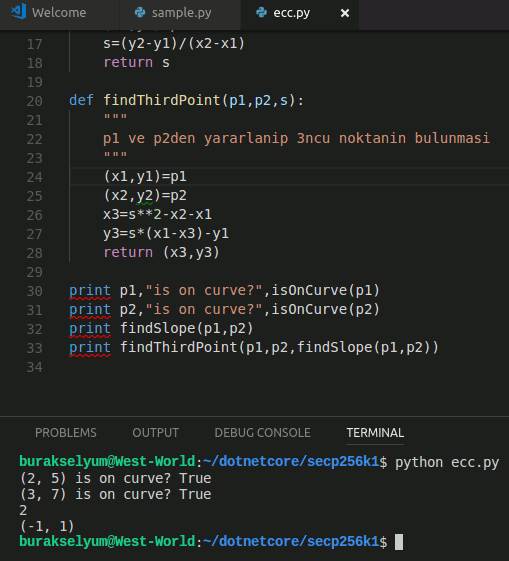
Python tarafına aşina olmayanlar için bile okunması oldukça kolay bir kod parçası görmektesiniz. x,y koordinatlarını işaret eden noktaları tuple tipi ile işaret etmekteyiz. Bu bir noktanın x ve y değerlerini taşırken veya elde ederken işlerimizi kolaylaştırmakta. isOnCurve fonksiyonu parametre olarak verilen noktanın eğri üzerinde olup olmadığını kontrol ediyor. findSlope metodu ile tahmin edeceğiniz üzere eğim değerini buluyoruz. findThirdPoint fonksiyonu p1 ve p2 parametrelerinden yararlanılarak p3ün yani 3ncü noktanın bulunmasında kullanılmakta. Kodu Visual Studio Code üzerinde geliştirebilirsiniz. Şahsen ben, öyle yaptım.
Eliptik Eğrilerin Gruplar ile İlişkisi
Eliptik eğriler ile matematik grupları arasında yakın ilişki vardır. Özellikle asallık söz konusu ise. Bunları bir eliptik eğri için düşündüğümüzde şunları söyleyebiliriz.
- G'yi noktaların olduğu bir grup olarak düşünürsek iki noktanın toplamı (P1 + P2 = P3) yine G'nin içinde yer alacaktır(Kapalılık özelliği)
- P1 + P2 + P3 = 0 aynı hat üzerinde 3 nokta söz konusu olduğunda toplam sonucu 0 olarak çıkar(Tabii noktaların hiçbirisi 0 olmayacak)
- Grubun mutlaka şu eşitliği sağlayan bir birim elemanı vardır ki eliptik eğriler için 0 olduğunu söyleyebiliriz. P1 + 0 = 0 + P1 = P1
- Her bir noktanın x ekseninde bir simetrisi vardır.
- Eğer değişebilirlik ( P1 + P2 = P2 + P1 ) söz konusu ise bu grup Abelian(Değişmeli diyebiliriz) olarak isimlendirilir(Abelian olmanın avantajları nelerdir halen araştırıyorum sevgili okur)
Grup olma özellikleri biraz sonra kriptografinin zorluğunu ortaya koyarken değer kazancak. Bu nedenle eliptik eğri kriptografisine geçmeden önce sonlu alanlara, asal sayılar nezninde de uğramamız gerekiyor.
Sonlu Alanlar
Artık eliptik eğrilerin nasıl bir denklem ile ifade edildiğini biliyoruz. Yazının başında Blockchain tarafından kullanılan denklemin grafiğini hatırlarsanız gerçek sayılar yerine toplam eleman sayısı bir asal sayı ile ifade edilen eliptik eğrinin söz konusu olduğunu belirtmiştik. Peki ne olaki bu sonlu alanlar(Finite Fields) Aşağıdaki gibi ifade edilen bir sayı dizisi olduğunu düşünelim(Aslında bizler için 0dan başlayan 13 elemanlı bir tamsayı dizisi)
F13 = {0, 1, 2, 3, … 12}
Bu dizilimin en önemli yanı 13 elemandan oluşması. 13 asal bir sayı. Dizinin bir diğer önemli özelliği de modüler aritmetik denklik kuramına göre içerideki iki sayının toplamının yine içerideki bir elemanı veriyor olması. Üstelik bu sadece toplama değil, çıkarma, çarpma ve bölme işlemleri için de geçerli bir durum. Sadece bölme işleminde kafaların biraz karışabildiği bir senaryo var ki burada da işin içerisine Fermat'nın Küçük Teorim(Fermat's Little Theorem) girmekte.
Toplama, çıkartma ve çarpma işlemlerine örnekler;
4 + 5 = 9 % 13 = 9 (Dizi içerisinde)
8 + 11 = 19 %13 = 6 (Dizi içerisinde)
8 - 12 = (-4) % 13 = 4 (Dizi içerisinde)
9 - 4 = 5 % 13 = 5 (Dizi içerisinde)
Gelelim bölme işlemine...
2 / 3 = 2 * 3-1 = 2 * 311 = 354.294 % 13 = 5 (Dizi içerisinde)
3 / 12 = 3 * 12-1 = 3 * 1211 = 2.229.025.112.064 % 13 = 10 (Dizi içerisinde)
İşlemler biraz tuhaf geldi değil mi? Özellike -1 üs değerinin eşitliğin devamında 13-2 şeklinde ifade edilmesi. Burada az önce bahsettiğimiz küçük teorimin büyük bir önemi var. Fermat'a göre p bir asal sayı, a bir tamsayı ve a ile p aralarında asal(p, a'nın bir çarpanı olamaz) iken
211 - 2 = 2046 % 11 = 0
gibi bir işlem'den bahsedilebilir. Modüler aritmetik notasyonuna göre ifade şudur.
ap ≡ a (mod p)
Buradan hareketle teoremin ispatı sırasında kullanılan Euler teoremine göre de
ap-1 ≡ 1 (mod p)
dir. Henüz ispatını araştıramamış olsam da bu denkliklerden yola çıkılarak şu ifadenin de doğru olduğu söylenmekte.
ap-2 ≡ a-1 ≡ 1/a (mod p)
Böylece bir bölme işleminin modüler aritmetik enstürmanlarına göre yine dizi içerisindeki bir elemanı işaret ettiğini görmüş oluyoruz.
Eliptik Eğrideki Ayrık Logaritma Problemi
Gelelim yukarıda anlattıklarımızı kullanarak neler yapabileceğimize bakmaya. Bir eliptik eğri üzerinde bir başlangıç noktası seçtiğimizi düşünelim. P olarak isimlendirelim(Sonradan Generator Point adına kavuşacak) Buna göre P'nin 1 katını, 2katını, 3katını ekleyerek devam edelim. Artık elimizde bir nokta grubu var ve onu şöyle ifade edebiliriz.
{0, P, 2P, 3P, 4P, 5P,... (n-1)P}
Çarpan olarak ele alınan n'nin gizli bir anahtar olduğunu düşündüğümüzde her ne kadar sP=Q değerini bulmak kolay olsa da P ve Q'yi bilip s'yi bulmaya çalıştığımız durumda bu o kadar da kolay olmayacaktır. Çünkü 0 ile n-1 arasındaki tüm olası değerleri göz önüne alıp eşitliğin sağlanıp sağlanmadığını anlamamız gerekir. Bunun sebebi ayrık logaritma problemi ile açıklanmaktadır.
Discrete Logarithm Problem
Aşağıdaki işlemi düşünelim.
329 mod 17 ≡ 12
Burada 12 değerine ulaşmak kolay. Fakat soru şu;
3x mod 17 ≡ 12
Burada x değerini nasıl bulabiliriz? Aslında 3ün olası üslerini taramak söz konusu eşitlikteki uygun x değerini bulmak için yeterli. Küçük bir asal sayı için bu çok büyük sorun teşkil etmeyecektir. Sorun 17 sayısı yerine çok çok çok büyük bir asal sayı geldiğinde ortaya çıkmaktadır. Teorikte mümkün ama pratiğe dökülmesi için asal değere göre dünyadaki işlemci gücünün tamamına sahip olsak bile çok uzun yıllar sürebilecek bir problem söz konusu(Uzmanların dilinden)
Tekrar P noktalarından oluşan grubumuza dönelim. Buradaki çarpan hesaplamaları için Double and Add algoritmasından yararlanılabilir.
Double and Add algorithm
Double and Add algoritmasında noktanın çarpanının ikilik sayı sistemindeki ifadesinden yararlanılır. Şöyle başlayalım. 19 asal sayısının ikilik sistemdeki karşılğı
10011
şeklindedir.
Bunu üssel gösterimle ifade etmek istersek şu eşitliği de yazabiliriz.
19 = 10011 = 1.24 + 0.23 + 0.22 + 1.21 + 1.20
Buna göre bir noktanın 19 ile çarpımını da şu şekilde ifade etmemiz mümkün hale gelir.
19P = 24P + 21P + 20P
Oluşan eşitliğe göre Double and Add algoritması şöyle işletilir.
P noktasını al.
Bunu 2ye katla(double). Bu sayede 2P değerini elde ederiz.
2P yi P ile topla(add) Böylece 21P + 20P değerini yakalarız.
...
Bu şekilde ikiye katlama ve toplama işlemlerinin tekrar edilmesi yoluyla sonuca ulaşabiliriz. Siz örneğin 151 sayısı için bu denkliği sağlamaya çalışarak konuyu pekiştirebilirsiniz. İpucu olarak başlangıçı veriyorum;
151 = 10010111 = 1.27 + 0.26 + 0.25 + 1.24 + 0.23 + 1.22 + 1.21 + 1.20 = 27 + 24 + 22 + 21 +20
Bir nokta grubu için tam sayı ile çarpma işlemini ele aldığımıza göre P grubu için şöyle bir örnek yapalım.
Denklemimiz y2 = x3 + 2x + 3
Sonlu alandaki toplam sayı adedi 17 (asaldır dikkat edin)
Başlangıç noktamız P(3,6)
Buna göre P'yi kendisi ile toplaya toplaya aşağıdaki dizilimi elde edebiliriz.
0P = 0
1P = (3,6)
2P = (12,2)
3P = (15,5)
4p = (14,2)
5P = (8,2)
6P = (8,15)
7P = (14,15)
8P = (15,12)
9P = (12,15)
10P = (3,11)
11P = (∞,∞)
12P = (3,6)
13P = (12,2)
14P =(15,5)
...
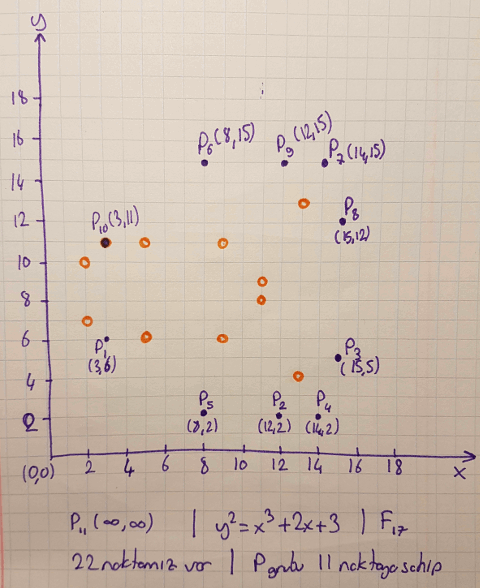
Bir şey dikkatinizi çekti mi? Toplamda denklemi sağlayan 22 adet (x,y) noktası söz konusu iken biz 11 elemanlı bir alt grup elde ettik ve bu grubun tekrar eden bir döngü içerisinde olduğunu görmekteyiz. Buradaki hesaplamalar için aşağıdaki örnek kod parçasını da kullanabiliriz. Fonksiyonları ve kullanım şekillerini anlamaya çalışın. İçeride bir de uzatılmış Euclid algoritması olarak isimlendirilmiş bir kısım var.
import collections
EllipticCurve = collections.namedtuple('EliptikEgri', 'name p a b g')
params = EllipticCurve(
'y^2=x^3+ax+b', #denklem
p=17, #toplam nokta sayisi
a=2, #denklem a degeri
b=3, #denklem b degeri
g=(3,6) #generator noktasi
)
def ReverseOfMod(n, p):
"""
n mod p isleminin tersini dondurur.
egim hesaplamasi isleminde p1 = p2 ve p1 != p2 durumlari icin gerekli
"""
if n == 0:
raise ZeroDivisionError('division by zero')
if n < 0:
# n ** -1 = p - (-n) ** -1 (mod p)
return p - ReverseOfMod(-n, p)
# Uzatilmis Euclid Algoritmasi uygulanir (Extended Euclidean Algorithm)
s, old_s = 0, 1
t, old_t = 1, 0
r, old_r = p, n
while r != 0:
d = old_r // r
old_r, r = r, old_r - d * r
old_s, s = s, old_s - d * s
old_t, t = t, old_t - d * t
gcd, x, y = old_r, old_s, old_t #gcd-greates common divisor - ebob
return x % p
def FindNegativePoint(p):
"""
negatif noktayi bulur
"""
if p is None:
return None
x, y = p
result = (x, -y % params.p)
return result
def Add(p1, p2):
"""
grup yasasindaki kriterlere gore p1+p1 islemini gerceklestirir
"""
if p1 is None:
# 0 + p2 = p2 durumu
return p2
if p2 is None:
# p1 + 0 = p1 durumu
return p1
x1, y1 = p1
x2, y2 = p2
if x1 == x2 and y1 != y2:
return None
if x1 == x2:
# p1==p2 durumu
m = (3 * x1 * x1 + params.a) * ReverseOfMod(2 * y1, params.p)
else:
# p1!=p2 durumu
m = (y1 - y2) * ReverseOfMod(x1 - x2, params.p)
x3 = m * m - x1 - x2
y3 = y1 + m * (x3 - x1)
result = (x3 % params.p,-y3 % params.p)
return result
def Multiply(n, p):
"""
n * P islemini gerceklestirir
"""
if n < 0:
return Multiply(-n, FindNegativePoint(p))
result = None
nextP = p
while n:
if n & 1:
result = Add(result, nextP)
nextP = Add(nextP, nextP)
n >>= 1
return result
for i in range(0,17):
print i,Multiply(i,(3,6))
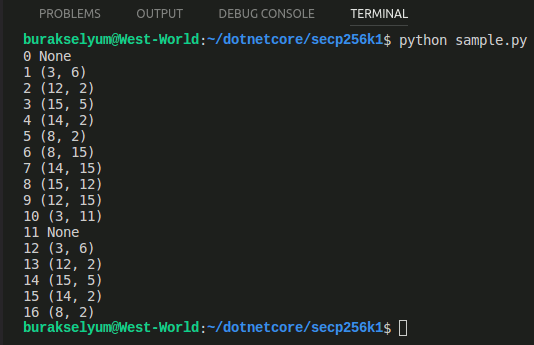
Nokta sahası sonlu uzunlukta ve çok doğal olarak alt grup da öyle. Ancak denklem ve asal sayı değeri dikkatli seçilirse çok büyük bir grubun elde edilmesi söz konusu olabilir. Öyle ki geri çevirlemeye çalışıldığında bu inanılmaz derecede zor olur.
Bitcoin Cephesi(secp256k1)
Onlar Blockchain'in bu kriptografi kuramını göz önüne alarak aşağıdaki parametreleri içeren bir eğri tanımlamışlar.
Denklem : y2=x3+7
Sonlu alan asal sayı değeri (p) = 2256 -232 - 29 -28 -27 -26 - 24 - 1
Giriş noktası G=( 79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8 )
Bir gruptaki asal nokta sayısı n = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
Dikkat edileceği üzere nokta ve asal sayı değerleri oldukça büyük. Bu da ayrık logaritma probleminin getireceği sorunun çözümünü oldukça zorlaştırır nitelikte. Her şeyden önce ortada 256bitlik bir asal sayı var. Bunun bir sonucu da en iyimser tahminle ortada 2256 olası gizli anahtarın olması ki herhangibirini tespit edebilmek için var olanlarından mümkün olduğunca çoğunu bilmek gerekiyor. Bunu anlatmak çok zor ama trilyonlarca yıl alabilecek bir zaman ortaya çıktığı söyleniyor(Teorik olarak)
Peki yazılımcı olarak biz bu değerleri kullanarak ne yapabiliriz? Aslında seçeceğimiz bir private key değeri ile public key üretebilir sonra bu iki anahtar bilgisinden yararlanarak dijital bir imza oluşturarak belgelerimizi kriptolayabiliriz. Bu amaçla kullanılabilecek pek çok kütüphane var. Hatta şu adreste güzel bir kod örneği de bulunmakta. İnceleyip denemenizi öneririm.
Sonuç
Eliptik Eğri denklemi Blockchain ve ondan türeyen pek çok yapı tarafından asimetrik şifre üretilip transaction'ların imzalanması maksadıyla kullanılmakta. Asitmerik şifrelemede public ve private olmak üzere iki anahtar söz konusu. Public Key herkes tarafından görülebilir bir bilgi ama private key tahmin edeceğiniz üzere kişiye özel. Private key değeri kullanılarak public key değerinin elde edilmesi mümkün. Bu değeri elde ederken yukarıdaki eliptik eğri denkleminden yararlanılmakta. Ancak public key değerini kullanarak private key bilgisine oluşturmak en azından önümüzdeki birkaç milyon yüz yıl(belki de fazlası) için mümkün değil. Blockchain bir transaction'ı imzalarken private key ile oluşturulmuş bir hash değeri kullanıyor. Hash bilgisinin geriye döndürülerek private key içeriğinin bulunması zaten mümkün değil lakin public key değerine sahip olan birisi kendi ürettiği private key'leri kullanarak oluşturacağı hash'leri karşılaştırmaya çalışabilir. Lakin burada onu bekleyen şey Eliptik Eğri Dijital Kriptografi Algoritması(Elliptic Curve Digital Signature Algorithm) oluyor; ki bu konu şu an için beni aşmakta. Kaynaklar arasında daha fazla kaybolmadan hatırladığım eski matematik denklemlerimi bir kenara bırakıyor ve hepinize mutlu günler diliyerek istirahata çekiliyorum.
Kaynaklar
Blockchain 101 - Foundational Math
Blockchain 101 - Elliptic Curve Cryptography
Modulo Denklik
MathWorl - Elliptic Curve
Learn Cryptography - CryptoCurrency(51 Attack)
Johannes Bauer - ECC
Andrea Corbellini - Elliptic Cure Cryptography - A Gentle Introduction
Andrea Corbellini - Elliptic Cure Cryptography - Finite Fields and Discrete Logarithms
Implementation of Elliptic Curve Digital Signature Algorithm
Elliptic Curve Scalar Multiplaction Calculator
BitcounWiki